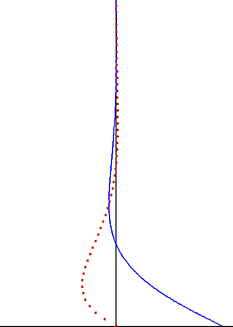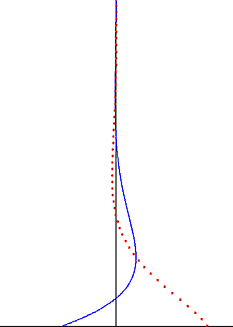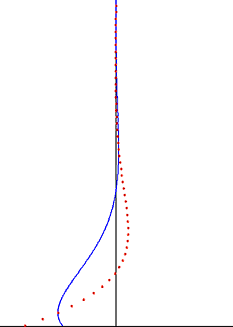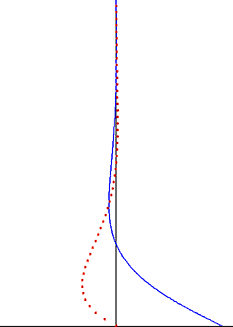
Stokesův problém - Stokes problem

Stokesův problém ve viskózní tekutině způsobený harmonickým kmitáním rovné tuhé desky (spodní černý okraj). Rychlost (modrá čára) a výchylka částic (červené tečky) jako funkce vzdálenosti ke zdi.

V dynamice tekutin je Stokesův problém známý také jako Stokesův druhý problém nebo někdy označovaný jako Stokesova mezní vrstva nebo oscilační mezní vrstva je problém určování toku vytvořeného oscilačním pevným povrchem, pojmenovaným po Siru George Stokesovi . To je považováno za jeden z nejjednodušších nestálých problémů, které mají přesné řešení pro Navier-Stokesovy rovnice . V turbulentním proudění se tomu stále říká Stokesova mezní vrstva, ale pro získání užitečných informací o toku se nyní musíme spoléhat na experimenty , numerické simulace nebo přibližné metody .

Popis toku

Vezměme si nekonečně dlouhou desku, která kmitá rychlostí ve směru, který je umístěn v nekonečné doméně tekutiny, kde je frekvence kmitání. Nestlačitelné Navier-Stokesovy rovnice se redukují na ${\ displaystyle U \ cos \ omega t}$ ${\ displaystyle x}$ ${\ displaystyle y = 0}$ ${\ displaystyle \ omega}$

{\ displaystyle {\ frac {\ částečné u} {\ částečné t}} = \ nu {\ frac {\ částečné ^ {2} u} {\ částečné y ^ {2}}}}

kde je kinematická viskozita . Tlakový gradient nevstupuje do problému. Počáteční neklouzavý stav na zdi je ${\ displaystyle \ nu}$

{\ Displaystyle u (0, t) = U \ cos \ omega t, \ quad u (\ infty, t) = 0,}

a druhá okrajová podmínka je způsobena skutečností, že pohyb není vnímán v nekonečnu. Průtok je způsoben pouze pohybem desky, nedochází k žádnému vynucenému tlakovému gradientu. ${\ displaystyle y = 0}$

Řešení

Počáteční podmínka není nutná z důvodu periodicity. Protože rovnice i okrajové podmínky jsou lineární, lze rychlost napsat jako skutečnou část nějaké složité funkce

{\ displaystyle u = U \ Re \ left [e ^ {i \ omega t} f (y) \ right]}

protože . ${\ displaystyle \ cos \ omega t = \ Re e ^ {i \ omega t}}$

Když to dosadíme do parciální diferenciální rovnice, sníží se to na obyčejnou diferenciální rovnici

{\ displaystyle f '' - {\ frac {i \ omega} {\ nu}} f = 0}

s okrajovými podmínkami

{\ displaystyle f (0) = 1, \ quad f (\ infty) = 0}

Řešení výše uvedeného problému je

{\ displaystyle f (y) = \ exp \ left [- {\ frac {1 + i} {\ sqrt {2}}} {\ sqrt {\ frac {\ omega} {\ nu}}} y \ right] }

{\ displaystyle u (y, t) = Ue ^ {- {\ sqrt {\ frac {\ omega} {2 \ nu}}} y} \ cos \ left (\ omega t - {\ sqrt {\ frac {\ omega} {2 \ nu}}} y \ doprava)}

Porucha způsobená oscilační deskou se šíří jako příčná vlna skrz tekutinu, ale je velmi tlumena exponenciálním faktorem. Hloubka průniku této vlny klesá s frekvencí oscilace, ale zvyšuje se s kinematickou viskozitou kapaliny. ${\ displaystyle \ delta = {\ sqrt {2 \ nu / \ omega}}}$

Síla na jednotku plochy působící na desku tekutinou je

{\ displaystyle F = \ mu \ left ({\ frac {\ částečné u} {\ částečné y}} \ pravé) _ {y = 0} = {\ sqrt {\ rho \ omega \ mu}} U \ cos \ vlevo (\ omega t - {\ frac {\ pi} {4}} \ vpravo)}

Mezi oscilací desky a vytvořenou silou dochází k fázovému posunu.

Oscilace vířivosti poblíž hranice

Důležitým postřehem ze Stokesova řešení pro oscilační Stokesův tok je, že oscilace vířivosti jsou omezeny na tenkou mezní vrstvu a exponenciálně vlhké, když se vzdalují od stěny. Toto pozorování platí také pro případ turbulentní mezní vrstvy. Mimo Stokesovu mezní vrstvu - která je často objemem tekutiny - mohou být oscilace vířivosti zanedbávány. Pro dobrou aproximaci jsou oscilace rychlosti toku mimo mezní vrstvu irotační a teorii potenciálního toku lze aplikovat na oscilační část pohybu. To významně zjednodušuje řešení těchto problémů s prouděním a často se používá v oblastech irrotačního proudění zvukových vln a vodních vln .

Tekutina ohraničená horní stěnou

Pokud je tekutinová doména ohraničena horní pevnou stěnou umístěnou ve výšce , je rychlost toku dána vztahem ${\ displaystyle y = h}$

{\ displaystyle u (y, t) = {\ frac {U} {2 (\ cosh 2 \ lambda h- \ cos 2 \ lambda h)}} [e ^ {- \ lambda (y-2h)} \ cos (\ omega t- \ lambda y) + e ^ {\ lambda (y-2h)} \ cos (\ omega t + \ lambda y) -e ^ {- \ lambda y} \ cos (\ omega t- \ lambda y +2 \ lambda h) -e ^ {\ lambda y} \ cos (\ omega t + \ lambda y-2 \ lambda h)]}

kde . ${\ displaystyle \ lambda = {\ sqrt {\ omega / (2 \ nu)}}}$

Tok v důsledku oscilačního gradientu tlaku v blízkosti rovné pevné desky

Stokesova mezní vrstva v důsledku sinusové oscilace rychlosti toku vzdáleného pole. Horizontální rychlost je modrá čára a odpovídající horizontální výchylky částic jsou červené tečky.

Pouzdro pro oscilační tok vzdáleného pole , s deskou drženou v klidu, lze snadno zkonstruovat z předchozího řešení pro oscilační desku pomocí lineární superpozice řešení. Zvažte rovnoměrnou oscilaci rychlosti daleko od desky a mizející rychlost na desce . Na rozdíl od stacionární tekutiny v původním problému musí být tlakový gradient zde v nekonečnu harmonickou funkcí času. Řešení je pak dáno ${\ displaystyle u (\ infty, t) = U _ {\ infty} \ cos \ omega t}$ ${\ displaystyle u (0, t) = 0}$

{\ displaystyle u (y, t) = U _ {\ infty} \ left [\, \ cos \ omega t - {\ text {e}} ^ {- {\ sqrt {\ frac {\ omega} {2 \ nu }}} y} \, \ cos \ left (\ omega t - {\ sqrt {\ frac {\ omega} {2 \ nu}}} y \ right) \ right],}

což je nula na zdi z = 0 , což odpovídá podmínce protiskluznosti pro zeď v klidu. S touto situací se často setkáváme ve zvukových vlnách v blízkosti pevné zdi nebo v případě pohybů tekutin v blízkosti mořského dna ve vodních vlnách . Vorticita, pro oscilační tok poblíž klidové stěny, se rovná vířivosti v případě oscilační desky, ale opačného znaménka.

Stokesův problém ve válcové geometrii

Torzní kmitání

Uvažujme nekonečně dlouhý válec o poloměru vykazující torzní oscilaci s úhlovou rychlostí, kde je frekvence. Poté se rychlost blíží po počáteční přechodné fázi k ${\ displaystyle a}$ ${\ displaystyle \ Omega \ cos \ omega t}$ ${\ displaystyle \ omega}$

{\ displaystyle v _ {\ theta} = a \ Omega \ \ Re \ left [{\ frac {K_ {1} (r {\ sqrt {i \ omega / \ nu}})}} {K_ {1} (a { \ sqrt {i \ omega / \ nu}}}} e ^ {i \ omega t} \ doprava]}

kde je upravená Besselova funkce druhého druhu. Toto řešení lze vyjádřit skutečným argumentem jako: ${\ displaystyle K_ {1}}$

{\ displaystyle {\ begin {aligned} v _ {\ theta} \ left (r, t \ right) & = \ Psi \ left \ lbrace \ left [{\ textrm {kei}} _ {1} \ left ({\ sqrt {R _ {\ omega}}} \ right) {\ textrm {kei}} _ {1} \ left ({\ sqrt {R _ {\ omega}}} r \ right) + {\ textrm {ker}} _ {1} \ left ({\ sqrt {R _ {\ omega}}} \ right) {\ textrm {ker}} _ {1} \ left ({\ sqrt {R _ {\ omega}}} r \ right) \ right] \ cos \ left (t \ right) \ right. \\ & + \ left. \ left [{\ textrm {kei}} _ {1} \ left ({\ sqrt {R _ {\ omega}}} \ vpravo) {\ textrm {ker}} _ {1} \ vlevo ({\ sqrt {R _ {\ omega}}} r \ vpravo) - {\ textrm {ker}} _ {1} \ vlevo ({\ sqrt { R _ {\ omega}}} \ right) {\ textrm {kei}} _ {1} \ left ({\ sqrt {R _ {\ omega}}} r \ right) \ right] \ sin \ left (t \ right ) \ right \ rbrace \\\ end {zarovnáno}}}

kde

{\ displaystyle \ Psi = \ left [{\ textrm {kei}} _ {1} ^ {2} \ left ({\ sqrt {R _ {\ omega}}} \ right) + {\ textrm {ker}} _ {1} ^ {2} \ left ({\ sqrt {R _ {\ omega}}} \ right) \ right] ^ {- 1},}

${\ displaystyle \ mathrm {kei}}$ a jsou Kelvina funkce a je na bezrozměrné oscilační Reynoldsova čísla definované jako , že kinematická viskozita. ${\ displaystyle \ mathrm {ker}}$ ${\ displaystyle R _ {\ omega}}$ ${\ displaystyle R _ {\ omega} = \ omega a ^ {2} / \ nu}$ ${\ displaystyle \ nu}$

Axiální oscilace

Pokud válec kmitá v axiálním směru rychlostí , pak je rychlostní pole ${\ displaystyle U \ cos \ omega t}$

{\ displaystyle u = U \ \ Re \ left [{\ frac {K_ {0} (r {\ sqrt {i \ omega / \ nu}})}} {K_ {0} (a {\ sqrt {i \ omega / \ nu}})}} e ^ {i \ omega t} \ vpravo]}

kde je upravená Besselova funkce druhého druhu. ${\ displaystyle K_ {0}}$

Průtok Stokes-Couette

V toku Couette bude místo translačního pohybu jedné z desek provedena oscilace jedné roviny. Pokud máme spodní stěnu v klidu a horní stěna v provádí oscilační pohyb s rychlostí , pak je rychlostní pole dáno vztahem ${\ displaystyle y = 0}$ ${\ displaystyle y = h}$ ${\ displaystyle U \ cos \ omega t}$

{\ displaystyle u = U \ \ Re \ doleva \ {{\ frac {\ sin ky} {\ sin kh}} \ doprava \}, \ quad {\ text {kde}} \ quad k = {\ frac {1 + i} {\ sqrt {2}}} {\ sqrt {\ frac {\ omega} {\ nu}}}.}

Třecí síla na jednotku plochy na pohybující se rovině je a na pevné rovině ano . ${\ displaystyle - \ mu U \ Re \ {k \ cot kh \}}$ ${\ displaystyle \ mu U \ Re \ {k \ csc kh \}}$

Viz také

Rayleighův problém

Reference

^ Wang, CY (1991). „Přesné řešení Navier-Stokesových rovnic v ustáleném stavu“. Roční přehled mechaniky tekutin . 23 : 159–177. Bibcode : 1991AnRFM..23..159W . doi : 10,1146 / annurev.fl.23.010191.001111 .
^ Landau a Lifshitz (1987), str. 83–85.
^ Batchelor, George Keith. Úvod do dynamiky tekutin. Cambridge University Press, 2000.
^ Lagerstrom, Paco Axel. Teorie laminárního proudění. Princeton University Press, 1996.
^ Acheson, David J. Elementární dynamika tekutin. Oxford University Press, 1990.
^ Landau, Lev Davidovich a Evgenii Michajlovič Lifshitz. „Mechanika tekutin.“ (1987).
^ Phillips (1977), str. 46.
^ Drazin, Philip G. a Norman Riley . Navier-Stokesovy rovnice: klasifikace toků a přesná řešení. Č. 334. Cambridge University Press, 2006.
^ Rivero, M .; Garzón, F .; Núñez, J .; Figueroa, A. "Studium toku indukovaného kruhovým válcem provádějícím torzní oscilaci". European Journal of Mechanics - B / Fluids . 78 : 245–251. doi : 10.1016 / j.euromechflu.2019.08.002 .
^ Landau, LD a Sykes, JB (1987). Fluid Mechanics: Vol 6. str. 88

[1] Wang, CY (1991). „Přesné řešení Navier-Stokesových rovnic v ustáleném stavu“. Roční přehled mechaniky tekutin . 23 : 159–177. Bibcode : 1991AnRFM..23..159W . doi : 10,1146 / annurev.fl.23.010191.001111 .

[2] Landau a Lifshitz (1987), str. 83–85.

[3] Batchelor, George Keith. Úvod do dynamiky tekutin. Cambridge University Press, 2000.

[4] Lagerstrom, Paco Axel. Teorie laminárního proudění. Princeton University Press, 1996.

[5] Acheson, David J. Elementární dynamika tekutin. Oxford University Press, 1990.

[6] Landau, Lev Davidovich a Evgenii Michajlovič Lifshitz. „Mechanika tekutin.“ (1987).

[Phil46-7] Phillips (1977), str. 46.

[8] Drazin, Philip G. a Norman Riley . Navier-Stokesovy rovnice: klasifikace toků a přesná řešení. Č. 334. Cambridge University Press, 2006.

[9] Rivero, M .; Garzón, F .; Núñez, J .; Figueroa, A. "Studium toku indukovaného kruhovým válcem provádějícím torzní oscilaci". European Journal of Mechanics - B / Fluids . 78 : 245–251. doi : 10.1016 / j.euromechflu.2019.08.002 .

[10] Landau, LD a Sykes, JB (1987). Fluid Mechanics: Vol 6. str. 88

Languages

In other projects