Lano (datová struktura) - Rope (data structure)

Jednoduché lano postavené na řetězci „Hello_my_name_is_Simon“.

V programování počítače , na laně , nebo kabelem , je datová struktura složená z menších řetězců , který se používá pro efektivní ukládání a manipulaci s velmi dlouhý řetězec. Například program pro úpravy textu může použít lano k reprezentaci upravovaného textu, takže lze efektivně provádět operace, jako je vkládání, mazání a náhodný přístup.

Popis

Lano je binární strom, kde každý list (koncový uzel) obsahuje řetězec a délku (také známou jako „váha“) a každý uzel dále na stromě drží součet délek všech listů v levém podstromu . Uzel se dvěma podřízenými tedy rozděluje celý řetězec na dvě části: levý podstrom ukládá první část řetězce, pravý podstrom ukládá druhou část řetězce a váha uzlu je délka první části.

U lanových operací se řetězce uložené v uzlech považují za konstantní neměnné objekty v typickém nedestruktivním případě, což umožňuje určité chování kopírování při zápisu . Uzly listu jsou obvykle implementovány jako základní řetězce pevné délky s připojeným počtem odkazů pro uvolnění, když už nejsou potřeba, i když lze použít i jiné metody uvolňování paměti .

Operace

V následujících definicích je N délka lana.

Vložit

Definice:: Insert(i, S’) vložte řetězec S ' začínající na pozici i do řetězce s , aby se vytvořil nový řetězec C 1 ,…, C i , S' , C i + 1 ,…, C m .
Časová složitost: .

Tuto operaci lze provést operacemi a Split() a dvěma Concat() . Cena je součtem všech tří.

Index

Obrázek 2.1: Příklad vyhledávání indexu na laně.
Definice:: Index(i) vrátit znak na pozici i
Časová složitost:

Chcete-li načíst i -tý znak, začneme rekurzivní vyhledávání z kořenového uzlu: 

function index(RopeNode node, integer i)
  if node.weight <= i and exists(node.right) then
    return index(node.right, i - node.weight)
  end
  
  if exists(node.left) then
    return index(node.left, i)
  end
  
  return node.string[i]
end

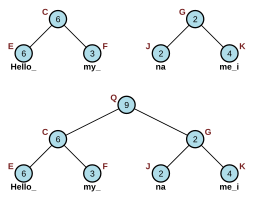
Chcete-li například najít znak na i=10 obrázku 2.1 zobrazeném vpravo, začněte v kořenovém uzlu (A), zjistěte, že 22 je větší než 10 a je zde levé dítě, takže přejděte na levé dítě (B). 9 je menší než 10, takže odečtěte 9 od 10 (opusťte i=1 ) a jděte k pravému dítěti (D). Protože je 6 větší než 1 a je zde levé dítě, přejděte k levému dítěti (G). 2 je větší než 1 a je zde levé dítě, takže jděte znovu k levému dítěti (J). Nakonec 2 je větší než 1, ale nezůstane žádné podřízené dítě, takže odpovědí je znak v indexu 1 krátkého řetězce „na“ (tj. „A“).

Concat

Obrázek 2.2: Zřetězení dvou dětských lan do jednoho lana.
Definice:: Concat(S1, S2) zřetězit dvě lana, S 1 a S 2 , do jednoho lana.
Časová složitost: (nebo čas pro výpočet hmotnosti kořene)

Zřetězení lze provést jednoduše vytvořením nového kořenového uzlu s left = S1 a right = S2 , což je konstantní čas. Váha nadřazeného uzlu je nastavena na délku levého podřízeného S 1 , což by vyžadovalo čas, pokud je strom vyvážený.

Jelikož většina lanových operací vyžaduje vyvážené stromy, může být nutné strom po vyrovnání znovu vyvážit.

Rozdělit

Obrázek 2.3: Rozdělení lana na polovinu.
Definice:: Split (i, S) rozdělte řetězec S na dva nové řetězce S 1 a S 2 , S 1 = C 1 ,…, C i a S 2 = C i + 1 ,…, C m .
Časová složitost:

Je třeba řešit dva případy:

  1. Bod rozdělení je na konci řetězce (tj. Za posledním znakem uzlu listu)
  2. Bod rozdělení je uprostřed řetězce.

Druhý případ se redukuje na první rozdělením řetězce v bodě rozdělení za účelem vytvoření dvou nových uzlů listu a poté vytvořením nového uzlu, který je nadřazeným řetězcem dvou komponent.

Chcete-li například rozdělit lano o délce 22 znaků zobrazené na obrázku 2.3 na dvě lana se stejnou složkou o délce 11, zadejte dotaz na 12. znak a vyhledejte uzel K na spodní úrovni. Odstraňte spojení mezi K a G . Přejděte na nadřazené G a odečíst hmotnost K z hmotnosti D . Projděte strom a vyjměte všechny pravé odkazy na podstromy pokrývající znaky za pozicí 11, odečtěte váhu K od jejich nadřazených uzlů ( v tomto případě pouze uzel D a A ). A konečně, vybudovat nově osamocených uzly K a H jejich zřetězení dohromady a vytvoření nového mateřský P s hmotností, která se rovná délce levého uzlu K .

Protože většina lanových operací vyžaduje vyvážené stromy, může být nutné strom po rozdělení znovu vyrovnat.

Vymazat

Definice:: Delete(i, j) odstranit podřetězec C i ,…, C i + j - 1 , ze s a vytvořit nový řetězec C 1 ,…, C i - 1 , C i + j ,…, C m .
Časová složitost: .

Tuto operaci lze provést dvěma Split() a jednou Concat() operací. Nejprve rozdělte lano na tři, vydělené i - tým a i + j -tým znakem, který extrahuje řetězec k odstranění v samostatném uzlu. Potom zřetězte další dva uzly.

Zpráva

Definice:: Report(i, j) výstup řetězce C i ,…, C i + j - 1 .
Časová složitost:

Chcete-li nahlásit řetězec C i ,…, C i + j - 1 , najděte uzel u, který obsahuje C i a weight(u) >= j , a poté projeďte T počínaje uzlem u . Výstup C i , ..., C i + j - 1 tím, že dělá přechodu přes in-pořadí z T začíná v uzlu u .

Srovnání s monolitickými poli

Výkon
Úkon Lano Tětiva
Index O (log n) O (1)
Rozdělit O (log n) O (1)
Zřetězit (destruktivně) O (log n) bez vyvážení / O (n) nejhorší případ Na)
Zřetězit (nedestruktivně) Na) Na)
Iterujte každou postavu Na) Na)
Vložit O (log n) bez vyvážení / O (n) nejhorší případ Na)
Připojit O (log n) bez vyvážení / O (n) nejhorší případ O (1) amortizován, O (n) nejhorší případ
Vymazat O (log n) Na)
Zpráva O (j + log n) O (j)
Stavět Na) Na)

Výhody:

  • Lana umožňují mnohem rychlejší vkládání a mazání textu než monolitická pole řetězců, u nichž mají operace časovou složitost O (n).
  • Lana nevyžadují O (n) extra paměť, když jsou provozována (pole to potřebují pro operace kopírování).
  • Lana nevyžadují velké souvislé paměťové prostory.
  • Pokud se používají pouze nedestruktivní verze operací, je lanko trvalou datovou strukturou . U příkladu programu pro úpravy textu to vede k snadné podpoře více úrovní zpět .

Nevýhody:

  • Větší celkové využití prostoru, když není provozováno, hlavně k ukládání nadřazených uzlů. Existuje kompromis mezi tím, kolik z celkové paměti je taková režie, a tím, jak dlouho se data zpracovávají jako řetězce. Řetězce na příkladech výše jsou pro moderní architektury nereálně krátké. Režie je vždy O (n), ale konstanta může být libovolně malá.
  • Prodloužení času pro správu dalšího úložiště
  • Zvýšená složitost zdrojového kódu; větší riziko chyb

Tato tabulka porovnává algoritmické vlastnosti implementací řetězců a lan, nikoli jejich surovou rychlost . Řetězce založené na poli mají menší režii, takže (například) operace zřetězení a rozdělení jsou u malých datových sad rychlejší. Pokud se však řetězce založené na poli používají pro delší řetězce, časová složitost a využití paměti pro vkládání a mazání znaků se stanou nepřijatelně velkými. Naproti tomu lanová datová struktura má stabilní výkon bez ohledu na velikost dat. Dále je prostorová složitost pro lana a pole O (n). Stručně řečeno, lana jsou vhodnější, když jsou data velká a často se mění.

Viz také

  • Cedar programovací prostředí, které používají provazy „téměř od svého vzniku“
  • Model T enfilade , podobnou datovou strukturu od začátku roku 1970.
  • Mezera vyrovnávací paměti , datová struktura běžně používaná v textových editorech, která umožňuje efektivní operace vkládání a mazání seskupené poblíž stejného místa
  • Kusová tabulka , další datová struktura běžně používaná v textových editorech

Reference

externí odkazy