Algoritmus řetězce nejbližších sousedů - Nearest-neighbor chain algorithm

V teorii Shluková analýza je algoritmu nejbližšího souseda řetězec je algoritmus , který může urychlit několik metod pro aglomerativní hierarchického shlukování . Jedná se o metody, které jako vstup berou kolekci bodů a vytvářejí hierarchii shluků bodů opakovaným slučováním dvojic menších klastrů a vytvářejí větší klastry. Mezi metody shlukování, pro které lze použít algoritmus řetězce nejbližšího souseda, patří Wardova metoda , klastrování úplných vazeb a klastrování s jedním spojením ; to vše funguje opakovaným slučováním nejbližších dvou klastrů, ale používají různé definice vzdálenosti mezi klastry. Vzdálenosti klastrů, pro které funguje algoritmus řetězce nejbližšího souseda, se nazývají redukovatelné a vyznačují se jednoduchou nerovností mezi určitými vzdálenostmi klastru.

Hlavní myšlenkou algoritmu je najít dvojice klastrů, které se mají sloučit, následováním cest v grafu nejbližšího souseda klastrů. Každá taková cesta nakonec skončí na dvojici klastrů, které jsou si navzájem nejblíže, a algoritmus vybere tuto dvojici klastrů jako dvojici ke sloučení. Aby se ušetřila práce opětovným použitím co nejvíce z každé cesty, používá algoritmus strukturu dat zásobníku pro sledování každé cesty, kterou sleduje. Algoritmus řetězu nejbližšího souseda tímto způsobem sloučí své klastry v jiném pořadí než metody, které vždy najdou a sloučí nejbližší dvojici klastrů. I přes tento rozdíl však vždy generuje stejnou hierarchii klastrů.

Algoritmus řetězce nejbližšího souseda konstruuje klastrování v čase úměrném druhé mocnině počtu bodů, které mají být seskupeny. To je také úměrné velikosti jeho vstupu, když je vstup poskytován ve formě explicitní matice vzdáleností . Algoritmus využívá množství paměti úměrné počtu bodů, když se používá pro metody shlukování, jako je Wardova metoda, která umožňuje výpočet vzdálenosti mezi klastry v konstantním čase. U některých jiných metod klastrování však využívá větší množství paměti v pomocné datové struktuře, se kterou sleduje vzdálenosti mezi dvojicemi klastrů.

Pozadí

Hierarchické seskupení šesti bodů. Body, které mají být seskupeny, jsou v horní části diagramu a uzly pod nimi představují shluky.

Mnoho problémů v analýze dat se týká klastrování , seskupování datových položek do klastrů blízce souvisejících položek. Hierarchické klastrování je verze klastrové analýzy, ve které klastry tvoří hierarchii nebo stromovou strukturu, nikoli přísný oddíl datových položek. V některých případech lze tento typ klastrování provádět jako způsob provádění klastrové analýzy ve více různých měřítcích současně. V jiných případech mají data, která mají být analyzována přirozeně, neznámou stromovou strukturu a cílem je obnovit tuto strukturu provedením analýzy. Oba tyto druhy analýz lze vidět například při aplikaci hierarchického shlukování do biologické taxonomie . V této aplikaci jsou různé živé věci seskupeny do shluků v různých měřítcích nebo úrovních podobnosti ( druh, rod, rodina atd. ). Tato analýza současně poskytuje víceúrovňové seskupení organismů současného věku a má za cíl přesně rekonstruovat proces větvení nebo evoluční strom, který v minulých dobách tyto organismy produkoval.

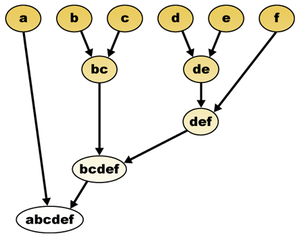
Vstup do problému shlukování se skládá ze sady bodů. Klastr je jakýkoliv vlastní podmnožinou z bodů, a hierarchické shlukování je maximální rodina klastrů s vlastností, že jakékoliv dva klastry v rodině jsou buď vnořené nebo disjunktní . Alternativně může být hierarchické shlukování reprezentováno jako binární strom s body na jeho listech; klastry shlukování jsou sady bodů v podstromech sestupně z každého uzlu stromu.

V aglomeračních klastrových metodách vstup také obsahuje funkci vzdálenosti definovanou na bodech nebo numerickou míru jejich odlišnosti. Vzdálenost nebo odlišnost by měla být symetrická: vzdálenost mezi dvěma body nezávisí na tom, který z nich je považován za první. Na rozdíl od vzdáleností v metrickém prostoru však není nutné, aby byla splněna nerovnost trojúhelníku . Dále se funkce podobnosti rozšíří z dvojic bodů na dvojice shluků. Různé metody klastrování provádějí toto rozšíření různými způsoby. Například v metodě klastrování s jedním spojením je vzdálenost mezi dvěma klastry definována jako minimální vzdálenost mezi libovolnými dvěma body z každého klastru. Vzhledem k této vzdálenosti mezi klastry může být hierarchické shlukování definováno chamtivým algoritmem, který zpočátku umístí každý bod do vlastního jednobodového klastru a poté opakovaně vytvoří nový klastr sloučením nejbližší dvojice klastrů.

Úzkým místem tohoto chamtivého algoritmu je podproblém najít, které dva klastry v každém kroku sloučit. Známé metody pro opakované hledání nejbližší dvojice klastrů v dynamické sadě klastrů buď vyžadují superlineární prostor pro udržení datové struktury, která dokáže rychle najít nejbližší dvojice, nebo jejich vyhledání nejbližšího páru zabere více než lineární čas. Algoritmus nejbližšího sousedního řetězce používá menší množství času a prostoru než chamtivý algoritmus sloučením dvojic klastrů v jiném pořadí. Tímto způsobem se vyhne problému opakovaného hledání nejbližších párů. Nicméně u mnoha typů problémů s klastrováním lze zaručit, že navzdory odlišnému pořadí sloučení přijdou se stejným hierarchickým shlukováním jako chamtivý algoritmus.

Algoritmus

Animace algoritmu pomocí Wardovy vzdálenosti. Černé tečky jsou body, šedé oblasti jsou větší shluky, modré šipky ukazují na nejbližší sousedy a červený pruh označuje aktuální řetězec. Pro vizuální jednoduchost, když sloučení ponechá řetězec prázdný, pokračuje v nedávno sloučeném clusteru.

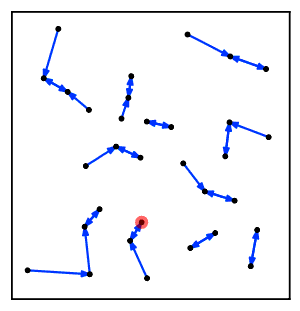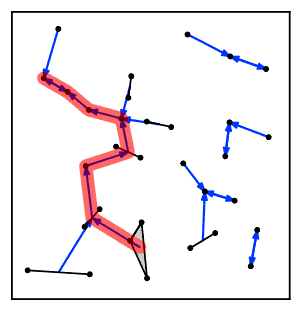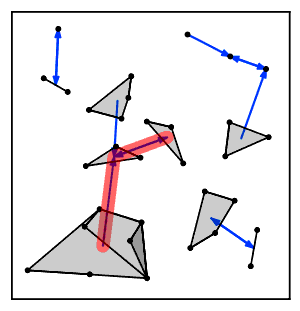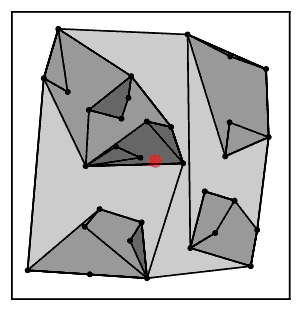
Intuitivně algoritmus nejbližšího sousedního řetězce opakovaně sleduje řetězec klastrů A → B → C → ... kde každý klastr je nejbližším sousedem předchozího, dokud nedosáhne dvojice klastrů, které jsou vzájemnými nejbližšími sousedy.

Podrobněji algoritmus provádí následující kroky:

• Inicializujte sadu aktivních klastrů tak, aby se skládala z n jednobodových klastrů, jednoho pro každý vstupní bod.
• Nechť S je datová struktura zásobníku , zpočátku prázdná, jejímiž prvky budou aktivní klastry.
• Zatímco v sadě klastrů je více než jeden klastr:
  • Pokud S je prázdný, zvolit aktivní clusteru libovolně a nasunout S .
  • Nechť C je aktivní clusteru na vrcholu S . Vypočítejte vzdálenosti od C ke všem ostatním klastrům a nechte D být nejbližší další klastr.
  • Pokud D je už v S musí být bezprostřední předchůdce C . Pop oba klastry od S a sloučit je.
  • V opačném případě, je-li D již není v S , nasunout S .

Když je možné, aby jeden klastr měl více stejných nejbližších sousedů, pak algoritmus vyžaduje konzistentní pravidlo pro přerušení. Například je možné všem klastrům přiřadit libovolná indexová čísla a poté vybrat (mezi stejnými nejbližšími sousedy) ten s nejmenším indexovým číslem. Toto pravidlo zabraňuje určitým druhům nekonzistentního chování v algoritmu; Například, aniž by toto pravidlo, sousední clusteru D může dojít dříve v zásobníku, než je předchůdce C .

Analýza času a prostoru

Každá iterace smyčky provede jediné hledání nejbližšího souseda klastru a buď přidá jeden klastr do zásobníku, nebo z něj odstraní dva klastry. Každý cluster je do zásobníku přidán pouze jednou, protože když je znovu odebrán, okamžitě se deaktivuje a sloučí. Do zásobníku se přidá celkem 2 n -2 klastry: n jednobodových klastrů v počáteční sadě a n -2 interní uzly jiné než kořen v binárním stromu představující shlukování. Algoritmus proto provádí 2 n - 2 tlačení iterací a n - 1 opakování iterací.

Každá z těchto iterací může strávit čas skenováním až n -1 meziklastrových vzdáleností, aby se našel nejbližší soused. Celkový počet výpočtů vzdálenosti, které provede, je tedy menší než 3 n ² . Ze stejného důvodu je celkový čas použitý algoritmem mimo tyto výpočty vzdáleností O ( n ² ) .

Protože jedinou datovou strukturou je sada aktivních klastrů a zásobník obsahující podmnožinu aktivních klastrů, požadovaný prostor je lineární v počtu vstupních bodů.

Správnost

Aby byl algoritmus správný, musí to být tak, že vyskakování a sloučení horních dvou klastrů ze zásobníku algoritmu zachovává vlastnost, že zbývající klastry v zásobníku tvoří řetězec nejbližších sousedů. Navíc by mělo platit, že všechny klastry vytvořené během algoritmu jsou stejné jako klastry vytvořené chamtivým algoritmem, který vždy sloučí nejbližší dva klastry, přestože chamtivý algoritmus obecně provede jeho sloučení v jiném pořadí než algoritmus řetězce nejbližšího souseda. Obě tyto vlastnosti závisí na konkrétní volbě způsobu měření vzdálenosti mezi klastry.

Správnost tohoto algoritmu závisí na vlastnosti jeho funkce vzdálenosti, která se nazývá redukovatelnost . Tuto vlastnost identifikoval Bruynooghe (1977) v souvislosti s dřívější metodou shlukování, která používala vzájemné páry nejbližších sousedů, ale nikoli řetězce nejbližších sousedů. Funkce vzdálenosti d na klastrech je definována jako redukovatelná, pokud pro každé tři klastry A , B a C v chamtivém hierarchickém shlukování tak, že A a B jsou vzájemní nejbližší sousedé, platí následující nerovnost:

d ( A ∪ B , C ) ≥ min (d ( A , C ), d ( B , C )) .

Pokud funkce vzdálenosti má tu vlastnost, převoditelnost, pak se spojení dvou klastrů C a D mohou způsobit pouze nejbližšího souseda E ke změně, pokud, že nejbližší soused byl jeden z C a D . To má pro algoritmus nejbližšího sousedního řetězce dva důležité důsledky. Za prvé, pomocí této vlastnosti lze ukázat, že v každém kroku algoritmu tvoří klastry na zásobníku S platný řetězec nejbližších sousedů, protože kdykoli se stane nejbližší soused neplatným, je okamžitě odebrán ze zásobníku.

Za druhé, a co je ještě důležitější, z této vlastnosti vyplývá, že pokud dva klastry C a D patří do chamtivého hierarchického shlukování a jsou vzájemnými nejbližšími sousedy v jakémkoli časovém okamžiku, pak budou sloučeny chamtivým shlukováním, protože musí zůstat vzájemnými nejbližšími sousedy, dokud nebudou sloučeni. Z toho vyplývá, že každý vzájemný pár nejbližších sousedů nalezený algoritmem nejbližšího sousedního řetězce je také dvojicí klastrů nalezených chamtivým algoritmem, a proto že algoritmus nejbližšího sousedního řetězce vypočítá přesně stejné shlukování (i když v jiném pořadí) jako chamtivý algoritmus.

Aplikace na konkrétní vzdálenosti clusterů

Wardova metoda

Wardova metoda je aglomerativní shlukovací metoda, ve které se odlišnost mezi dvěma klastry A a B měří podle velikosti, o kterou by sloučení dvou klastrů do jednoho většího klastru zvýšilo průměrnou čtvercovou vzdálenost bodu k jeho těžisku v klastru . To znamená,

${\ Displaystyle d (A, B) = \ sum _ {x \ in A, y \ in B} {\ frac {d^{2} (x, y)} {| A |+| B |}}-- \ sum _ {x, y \ v A} {\ frac {d^{2} (x, y)} {| A |}}-\ sum _ {x, y \ v B} {\ frac {d^ {2} (x, y)} {| B |}}.}$

Vyjádřeno těžištěm a mohutností obou shluků má jednodušší vzorec ${\ displaystyle c_ {A}}$ ${\ displaystyle n_ {A}}$

${\ Displaystyle d (A, B) = {\ frac {d^{2} (c_ {a}, c_ {b})} {1/n_ {A}+1/n_ {B}}},}$

což umožňuje jeho výpočet v konstantním čase na výpočet vzdálenosti. Ačkoli je Wardova metoda velmi citlivá na odlehlé hodnoty , je nejpopulárnější variací aglomerativního shlukování, a to jak kvůli kulatému tvaru klastrů, které obvykle tvoří, tak kvůli principiální definici shlukování, které má v každém kroku nejmenší rozptyl v rámci svých klastrů. Alternativně lze tuto vzdálenost považovat za rozdíl v k-průměrných nákladech mezi novým klastrem a dvěma starými klastry.

Wardova vzdálenost je také redukovatelná, jak je snadněji vidět z jiného vzorce pro výpočet vzdálenosti sloučeného klastru ze vzdáleností klastrů, ze kterých byl sloučen:

${\ Displaystyle d (A \ cup B, C) = {\ frac {n_ {A}+n_ {C}} {n_ {A}+n_ {B}+n_ {C}}} d (A, C) +{\ frac {n_ {B}+n_ {C}} {n_ {A}+n_ {B}+n_ {C}}} d (B, C)-{\ frac {n_ {C}} {n_ {A}+n_ {B}+n_ {C}}} d (A, B).}$

Vzorce pro aktualizaci vzdálenosti, jako je tento, se po práci Lance & Williamse (1967) nazývají vzorce „typu Lance – Williams“ . Pokud je nejmenší ze tří vzdáleností na pravé straně (což by nutně platilo, kdyby a jsou vzájemnými nejbližšími sousedy), pak je negativní příspěvek z jeho termínu zrušen koeficientem jednoho ze dvou dalších výrazů, přičemž zůstane kladné hodnota přidaná k váženému průměru ostatních dvou vzdáleností. Kombinovaná vzdálenost je proto vždy alespoň tak velká jako minimum a , což odpovídá definici redukovatelnosti. ${\ displaystyle d (A, B)}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle n_ {C}}$${\ displaystyle d (A, C)}$${\ displaystyle d (B, C)}$

Protože Wardova vzdálenost je redukovatelná, algoritmus nejbližšího sousedního řetězce využívající Wardovu vzdálenost vypočítá přesně stejné shlukování jako standardní chamtivý algoritmus. Pro n bodů v euklidovském prostoru konstantní dimenze je potřeba čas O ( n ² ) a prostor O ( n ) .

Kompletní propojení a průměrná vzdálenost

Klastrování s úplným propojením nebo nejvzdálenějším sousedem je forma aglomerativního shlukování, které definuje odlišnost mezi klastry jako maximální vzdálenost mezi libovolnými dvěma body ze dvou klastrů. Podobně klastrování průměrné vzdálenosti používá průměrnou párovou vzdálenost jako odlišnost. Stejně jako Wardova vzdálenost se tyto dvě formy shlukování řídí vzorcem typu Lance -Williamse. V úplném propojení je vzdálenost maximální ze dvou vzdáleností a . Proto je přinejmenším roven minimu těchto dvou vzdáleností, požadavku na to, aby byl redukovatelný. Pro průměrnou vzdálenost je pouze vážený průměr vzdáleností a . Opět platí, že je to minimálně stejně velké jako minimum ze dvou vzdáleností. V obou těchto případech je tedy vzdálenost redukovatelná. ${\ Displaystyle d (A \ cup B, C)}$${\ displaystyle d (A, C)}$${\ displaystyle d (B, C)}$${\ Displaystyle d (A \ cup B, C)}$${\ displaystyle d (A, C)}$${\ displaystyle d (B, C)}$

Na rozdíl od Wardovy metody tyto dvě formy shlukování nemají metodu pro výpočet vzdáleností mezi dvojicemi klastrů v konstantní době. Místo toho je možné udržovat řadu vzdáleností mezi všemi páry klastrů. Kdykoli jsou dva klastry sloučeny, vzorec lze použít k výpočtu vzdálenosti mezi sloučeným klastrem a všemi ostatními klastry. Udržování tohoto pole v průběhu algoritmu klastrování vyžaduje čas a prostor O ( n ² ) . Algoritmus nejbližšího sousedního řetězce může být použit ve spojení s tímto polem vzdáleností k nalezení stejného shlukování jako chamtivý algoritmus pro tyto případy. Jeho celkový čas a prostor pomocí tohoto pole je také O ( n ² ) .

Stejných časových a prostorových hranic O ( n ² ) lze také dosáhnout odlišným způsobem, a to technikou, která překrývá datovou strukturu prioritní fronty na bázi kvadrantu nad maticí vzdáleností a používá ji k provádění standardního algoritmu chamtivého shlukování. Tato metoda quadtree je obecnější, protože funguje i pro metody klastrování, které nejsou redukovatelné. Algoritmus nejbližšího sousedního řetězce však odpovídá jeho časovým a prostorovým hranicím při použití jednodušších datových struktur.

Jednoduché propojení

Při klastrování s jedním spojením nebo nejbližším sousedem, nejstarší formou aglomerativního hierarchického shlukování, se odlišnost mezi klastry měří jako minimální vzdálenost mezi libovolnými dvěma body od těchto dvou klastrů. S touto nepodobností

${\ Displaystyle d (A \ cup B, C) = \ min (d (A, C), d (B, C)),}$

splnění požadavku redukovatelnosti jako rovnosti spíše než nerovnosti. (Jednovazný také dodržuje Lance-Williamsův vzorec, ale s negativním koeficientem, ze kterého je obtížnější prokázat redukovatelnost.)

Stejně jako u úplného propojení a průměrné vzdálenosti, obtížnost výpočtu vzdáleností klastru způsobí, že algoritmu nejbližšího sousedního řetězce zabere čas a prostor O ( n ² ) výpočet jednolinkového shlukování. Nicméně, jeden-vazba shlukování lze nalézt efektivněji alternativní algoritmus, který počítá minimální kostra vstupních vzdáleností pomocí Prim algoritmu , a potom seřadí minimální klenout hrany stromu a tento seřazený seznam jako vodítko pro spojení párů klastry. V rámci Primova algoritmu lze každou následnou minimální hranu překlenovacího stromu nalézt sekvenčním vyhledáváním v netříděném seznamu nejmenších hran spojujících částečně vytvořený strom s každým dalším vrcholem. Tato volba šetří čas, který by jinak algoritmus strávil úpravou váhy vrcholů ve své prioritní frontě . Použití Primova algoritmu tímto způsobem by vyžadovalo čas O ( n ² ) a prostor O ( n ) , čímž by se shodovaly nejlepší hranice, kterých by bylo možné dosáhnout pomocí algoritmu nejbližšího sousedního řetězce pro vzdálenosti s výpočty s konstantním časem.

Těžiště vzdálenost

Dalším měřítkem vzdálenosti běžně používaným v aglomeračním shlukování je vzdálenost mezi centroidy dvojic shluků, známá také jako metoda vážené skupiny. Lze jej snadno vypočítat za konstantní čas na výpočet vzdálenosti. Není však redukovatelný. Pokud například vstup tvoří sadu tří bodů rovnostranného trojúhelníku, sloučení dvou těchto bodů do většího klastru způsobí zmenšení vzdálenosti mezi klastry, což je porušení redukovatelnosti. Algoritmus nejbližšího sousedního řetězce proto nemusí nutně najít stejné shlukování jako chamtivý algoritmus. Přesto Murtagh (1983) píše, že řetězový algoritmus nejbližšího souseda poskytuje „těžkou heuristiku“ pro metodu těžiště. K nalezení chamtivého shlukování v čase O ( n ² ) lze pro toto měření vzdálenosti použít jiný algoritmus od Day & Edelsbrunner (1984) .

Vzdálenosti citlivé na sloučení objednávky

Výše uvedená prezentace výslovně nepovolila vzdálenosti citlivé na sloučení objednávky. Povolení takových vzdáleností může skutečně způsobit problémy. Zejména existují vzdálenosti clusterů citlivé na pořadí, které splňují redukovatelnost, ale pro které výše uvedený algoritmus vrátí hierarchii se suboptimálními náklady. Proto když jsou vzdálenosti klastru definovány rekurzivním vzorcem (jako jsou některé z výše diskutovaných), je třeba dbát na to, aby nepoužívali hierarchii způsobem, který je citlivý na sloučení pořadí.

Dějiny

Algoritmus řetězce nejbližšího souseda byl vyvinut a implementován v roce 1982 Jean-Paulem Benzécriem a J. Juanem. Tento algoritmus založili na dřívějších metodách, které konstruovaly hierarchické shlukování pomocí vzájemných párů nejbližších sousedů, aniž by využívaly výhod řetězců nejbližšího souseda.

Reference