Křižovatka - Intersection

Kruh (černá) protíná čáru (purpurové) ve dvou bodech (červená). Disk (žlutý) protíná čáru v úsečce mezi dvěma červenými body.

Křižovatka (červená) dvou disků (bílá a červená s černými hranicemi).

Průsečík D a E je znázorněn šedavě purpurově. Průsečík A s kterýmkoli z B, C, D nebo E je prázdná množina .

V matematice je průnik dvou nebo více objektů dalším, obvykle „menším“ objektem. Intuitivně je průsečíkem předmětů to, co patří všem. Například v euklidovské geometrii platí , že když dvě čáry v rovině nejsou rovnoběžné, je jejich průsečíkem bod, ve kterém se setkají. Obecněji je v teorii množin průnik množin definován jako množina prvků, které patří všem. Na rozdíl od euklidovské definice to nepředpokládá, že by uvažované objekty ležely ve společném prostoru .

Křižovatka je jedním ze základních pojmů geometrie . Průsečík může mít různé geometrické tvary , ale bod je v rovinné geometrii nejběžnější . Geometrie incidentů definuje průsečík (obvykle z ploch ) jako objekt nižší dimenze, který dopadá na každý z původních objektů. V tomto přístupu může být křižovatka někdy nedefinovaná, například pro rovnoběžné čáry . V obou případech koncept křižovatky závisí na logické konjunkci . Algebraická geometrie definuje průsečíky svým vlastním způsobem s teorií průniku .

Jedinečnost

Může existovat více než jeden primitivní objekt, například body (na obrázku výše), které tvoří průsečík. Na křižovatku lze pohlížet souhrnně jako na všechny sdílené objekty (tj. Operace křížení má za následek množinu , možná prázdnou) nebo jako několik křižovatkových objektů ( možná nula ).

V teorii množin

Vzhledem k tomu, že silnice odpovídá sadě všech jejích umístění, silniční křižovatka (azurová) dvou silnic (zelená, modrá) odpovídá průsečíku jejich sad.

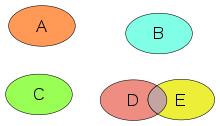
Průsečík dvou množin A a B je množina prvků, které jsou v obou A a B . V symbolech,

${\ Displaystyle A \ cap B = \ {x: x \ in A {\ text {a}} x \ in B \}}$.

Pokud například platí A = {1, 3, 5, 7} a B = {1, 2, 4, 6}, pak A ∩ B = {1}. Propracovanější příklad (zahrnující nekonečné množiny) je:

A = { x je sudé celé číslo }

B = { x je celé číslo dělitelné 3}

${\ Displaystyle A \ cap B = \ {6,12,18, \ dots \}}$

Jako další příklad číslo 5 není obsaženo v průniku množiny prvočísel {2, 3, 5, 7, 11, ...} a množiny sudých čísel {2, 4, 6, 8, 10,… }, protože ačkoli 5 je prvočíslo, není sudé. Ve skutečnosti je číslo 2 jediným číslem v průsečíku těchto dvou sad. V tomto případě má průnik matematický význam: číslo 2 je jediné sudé prvočíslo.

V euklidovské geometrii

• Křižovatka přímka - čára
• Průsečík přímka - rovina
• Průsečík čára - koule
• Průsečík mnohostěnu s přímkou
• Křižovatka úseček
• Křižovatková křivka

Zápis

Křižovatka je označena U+2229 ∩ INTERSECTION od Unicode Mathematical Operators .

Symbol U+2229 ∩ byl poprvé použit Hermannem Grassmannem v Die Ausdehnungslehre von 1844 jako obecný provozní symbol, nespecializovaný na křižovatku. Odtud jej použil Giuseppe Peano (1858-1932) k křižovatce, v roce 1888 v Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann .

Peano také vytvořil velké symboly pro obecné křižovatky a spojení více než dvou tříd ve své knize Formulario mathematico z roku 1908 .

Viz také

• Konstruktivní objemová geometrie , Boolean Intersection je jedním ze způsobů kombinování 2D/3D tvarů
• Rozměrově rozšířený 9-průsečíkový model
• Meet (mřížová teorie)

Reference

externí odkazy

• Weisstein, Eric W. „Křižovatka“ . MathWorld .