Grahamovo skenování - Graham scan

Ukázka Grahamova skenu k nalezení 2D konvexního trupu.

Grahamovo skenování je metoda hledání konvexního trupu konečné sady bodů v rovině s časovou složitostí O ( n log n ). Je pojmenován po Ronaldovi Grahamovi , který publikoval původní algoritmus v roce 1972. Algoritmus najde všechny vrcholy konvexního trupu uspořádaného podél jeho hranice. Využívá zásobník k efektivní detekci a odstranění konkávností na hranici.

Algoritmus

Jak je vidět, PAB a ABC jsou proti směru hodinových ručiček, ale BCD není. Algoritmus detekuje tuto situaci a zahodí dříve vybrané segmenty, dokud není provedený tah proti směru hodinových ručiček (v tomto případě ABD).

Prvním krokem v tomto algoritmu je nalezení bodu s nejnižší souřadnicí y. Pokud nejnižší souřadnice y existuje ve více než jednom bodě sady, měl by být vybrán bod s nejnižší souřadnicí x z kandidátů. Nazývají tento bod P . Tento krok trvá O ( n ), kde n je počet dotyčných bodů.

Dále musí být sada bodů seřazena ve vzestupném pořadí úhlu, který spolu s bodem P tvoří s osou x. K tomu je vhodný jakýkoli univerzální třídicí algoritmus , například heapsort (což je O ( n log n )).

Třídění podle úhlu nevyžaduje výpočet úhlu. Je možné použít jakoukoli funkci úhlu, která je v intervalu monotónní . Kosinus lze snadno vypočítat pomocí bodového součinu , nebo lze použít sklon čáry. Pokud jde o číselnou přesnost, může funkce porovnání použitá algoritmem třídění použít k určení relativních úhlů znaménko křížového součinu . ${\ displaystyle [0, \ pi]}$

Algoritmus pokračuje zvážením každého z bodů v seřazeném poli v pořadí. U každého bodu se nejprve určí, zda cestování ze dvou bodů bezprostředně předcházejících tomuto bodu představuje odbočení vlevo nebo vpravo. Pokud se jedná o zatáčku doprava, předposlední bod není součástí konvexního trupu a leží „uvnitř“. Stejné určení se pak provede pro množinu posledního bodu a dva body, které bezprostředně předcházejí bodu, o kterém se zjistilo, že byl uvnitř trupu, a opakuje se, dokud nenarazí na sadu „otočení doleva“, kdy se algoritmus posune dál do dalšího bodu v sadě bodů v seřazeném poli minus všechny body, u kterých bylo zjištěno, že jsou uvnitř trupu; není třeba tyto body znovu zvažovat. (Pokud jsou v kterékoli fázi tři body kolineární, lze se rozhodnout buď zahodit, nebo to nahlásit, protože v některých aplikacích je nutné najít všechny body na hranici konvexního trupu.)

Opět platí, že určení, zda tři body tvoří „odbočku doleva“ nebo „odbočku doprava“, nevyžaduje výpočet skutečného úhlu mezi dvěma úsečkami a lze ji ve skutečnosti dosáhnout pouze jednoduchou aritmetikou. U třech bodech , a , vypočítat Z -coordinate o součin těchto dvou vektorů a , což je dáno výrazem . Pokud je výsledek 0, body jsou kolineární; pokud je kladná, tvoří tři body orientaci „doleva“ nebo proti směru hodinových ručiček, jinak „doprava“ nebo orientaci ve směru hodinových ručiček (pro body očíslované proti směru hodinových ručiček). ${\ displaystyle P_ {1} = (x_ {1}, y_ {1})}$${\ displaystyle P_ {2} = (x_ {2}, y_ {2})}$${\ displaystyle P_ {3} = (x_ {3}, y_ {3})}$ ${\ displaystyle {\ overrightarrow {P_ {1} P_ {2}}}}$${\ displaystyle {\ overrightarrow {P_ {1} P_ {3}}}}$${\ displaystyle (x_ {2} -x_ {1}) (y_ {3} -y_ {1}) - (y_ {2} -y_ {1}) (x_ {3} -x_ {1})}$

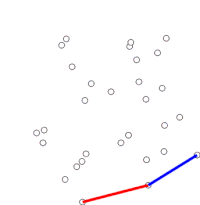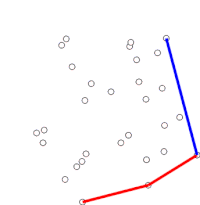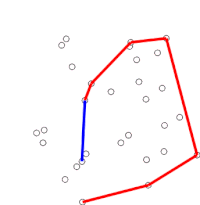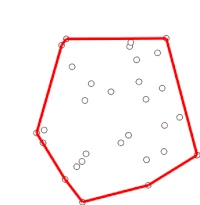
Tento proces se nakonec vrátí do bodu, ve kterém začal, kdy je algoritmus dokončen a zásobník nyní obsahuje body na konvexním trupu v pořadí proti směru hodinových ručiček.

Časová složitost

Třídění bodů má časovou složitost O ( n log n ). I když se může zdát, že časová složitost smyčky je O ( n ² ), protože pro každý bod se vrací zpět, aby se zkontrolovalo, zda některý z předchozích bodů „zatočil doprava“, je to vlastně O ( n ), protože každý bod je v určitém smyslu považován maximálně dvakrát. Každý bod se může objevit pouze jednou jako bod v „zatáčce doleva“ (protože algoritmus postupuje do dalšího bodu poté) a jako bod v „zatáčce vpravo“ (protože bod je odstraněn). Celková časová složitost je tedy O ( n log n ), protože čas třídění dominuje času skutečně vypočítat konvexní trup. ${\ displaystyle (x_ {2}, y_ {2})}$${\ displaystyle (x_ {3}, y_ {3})}$${\ displaystyle (x_ {2}, y_ {2})}$${\ displaystyle (x_ {2}, y_ {2})}$

Pseudo kód

Níže uvedený kód používá funkci ccw: ccw> 0, pokud se tři body otočí proti směru hodinových ručiček, ve směru hodinových ručiček, pokud ccw <0, a kolineární, pokud ccw = 0. (V reálných aplikacích, pokud jsou souřadnice libovolná reálná čísla, funkce vyžaduje přesné srovnání čísel s plovoucí desetinnou čárkou a je třeba si dávat pozor na numerické singularity pro „téměř“ kolineární body.)

Poté nechte výsledek uložit do stack.

let points be the list of points
let stack = empty_stack()

find the lowest y-coordinate and leftmost point, called P0
sort points by polar angle with P0, if several points have the same polar angle then only keep the farthest

for point in points:
    # pop the last point from the stack if we turn clockwise to reach this point
    while count stack > 1 and ccw(next_to_top(stack), top(stack), point) <= 0:
        pop stack
    push point to stack
end

Zásobník nyní obsahuje konvexní trup, kde jsou body orientovány proti směru hodinových ručiček a P0 je první bod.

Tady next_to_top()je funkce pro vrácení položky o jeden záznam pod horní část zásobníku, aniž by se změnil zásobník, a podobně top()pro vrácení nejvyššího prvku.

Tento pseudokód je upraven z Úvod do algoritmů .

Poznámky

Stejná základní myšlenka funguje také v případě, že je vstup tříděn na souřadnici x namísto úhlu a trup je vypočítán ve dvou krocích, které vytvářejí horní a dolní část trupu. Tuto úpravu navrhl AM Andrew a je znám jako Andrewův monotónní řetězový algoritmus . Má stejné základní vlastnosti jako Grahamovo skenování.

Zásobník technika používaná v testu Grahamova je velmi podobný tomu, který pro všechny nejbližší menší hodnoty problém, a mohou být také použity paralelní algoritmy pro všechny menší nejbližších hodnot (jako Grahama skenování) účinně vypočítat konvexní obal vytříděných sekvencí bodů.

Numerická robustnost

Numerická robustnost je problém, který je třeba řešit v algoritmech, které používají počítačovou aritmetiku s plovoucí desetinnou čárkou s konečnou přesností . Dokument z roku 2004 analyzoval jednoduchou přírůstkovou strategii, kterou lze použít zejména pro implementaci Grahamova skenu. Uvedeným cílem příspěvku nebylo konkrétně analyzovat algoritmus, ale spíše poskytnout učebnicový příklad toho, co a jak může selhat kvůli výpočtům s plovoucí desetinnou čárkou ve výpočetní geometrii . Později to vypracovali D. Jiang a NF Stewart a pomocí zpětné analýzy chyb učinili dva hlavní závěry. První je, že konvexní trup je dobře podmíněným problémem, a proto lze očekávat algoritmy, které vytvoří odpověď v rozumné míře chyby. Zadruhé prokazují, že modifikace Grahamova skenování, které nazývají Graham-Fortune (zahrnující myšlenky Stevena Fortunea na numerickou stabilitu), překonává problémy konečné přesnosti a nepřesných údajů „v jakémkoli rozsahu je to možné“.

Viz také

• Konvexní trupové algoritmy

Reference

Další čtení

• Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein, Clifford (2001) [1990]. „33.3: Nalezení konvexního trupu“. Úvod do algoritmů (2. vyd.). MIT Press a McGraw-Hill. 949–955. ISBN 0-262-03293-7.