Výpočetní anatomie - Computational anatomy

Výpočetní anatomie je interdisciplinární obor biologie zaměřený na kvantitativní zkoumání a modelování variability anatomických tvarů. Zahrnuje vývoj a aplikaci matematických, statistických a datově analytických metod pro modelování a simulaci biologických struktur.

Obor je široce definován a zahrnuje základy anatomie , aplikované matematiky a čisté matematiky , strojového učení , výpočetní mechaniky , výpočetní vědy , biologického zobrazování , neurovědy , fyziky , pravděpodobnosti a statistiky ; má také silné spojení s mechanikou tekutin a geometrickou mechanikou . Navíc doplňuje novější, interdisciplinární obory, jako jsou bioinformatika a neuroinformatika, v tom smyslu, že jeho interpretace využívá metadata odvozená z původních senzorových zobrazovacích modalit ( jedním z příkladů je zobrazování magnetickou rezonancí ). Zaměřuje se spíše na zobrazované anatomické struktury než na lékařská zobrazovací zařízení. V duchu se podobá historii počítačové lingvistiky , disciplíně, která se zaměřuje spíše na lingvistické struktury než na senzory fungující jako přenosová a komunikační média.

Ve výpočetní anatomii se skupina diffeomorphism používá ke studiu různých souřadnicových systémů prostřednictvím transformací souřadnic generovaných pomocí Lagrangian a Eulerian rychlosti proudění v . Tyto ve výpočetní anatomii toky mezi souřadnicemi jsou omezeny být geodetické toky splňují princip nejmenší akce pro kinetické energie proudu . Kinetická energie je definována Sobolevovou normou hladkosti s přísně více než dvěma generalizovanými, čtvercově integrovatelnými deriváty pro každou složku rychlosti proudění, což zaručuje, že toky jsou diffeomorfismy. Z toho také vyplývá, že hybnost tvarů diffeomorfního tvaru získaná bodově uspokojující Euler-Lagrangeovu rovnici pro geodetiku je určena jejími sousedy prostřednictvím prostorových derivací na rychlostním poli. To odděluje disciplínu od případu nestlačitelných tekutin, pro které je hybnost bodovou funkcí rychlosti. Výpočetní anatomie protíná studium riemannianských variet a nelineární globální analýzy , kde jsou středem zájmu skupiny diffeomorphismů. Rozvíjející se vysokodimenzionální teorie tvaru jsou ústředním bodem mnoha studií ve výpočetní anatomii, stejně jako otázky vyplývající z rodící se oblasti tvarové statistiky . Metrické struktury ve výpočetní anatomii v duchu souvisejí s morfometrií , s tím rozdílem, že výpočetní anatomie se zaměřuje na nekonečně dimenzionální prostor souřadnicových systémů transformovaných diffeomorphismem , a proto je centrální použití terminologie diffeomorphometry , studium metrického prostoru souřadných systémů prostřednictvím diffeomorphismů. ${\ displaystyle {\ mathbb {R}}^{3}}$${\ displaystyle \ mathbb {R} ^{3}}$

Genesis

Srdcem výpočetní anatomie je srovnání tvaru rozpoznáváním v jednom tvaru druhého. To jej spojuje s vývojem D'Arcy Wentwortha Thompsona o růstu a formě, který vedl k vědeckému vysvětlení morfogeneze , procesu, kterým se v biologii vytvářejí vzorce . Čtyři knihy Albrechta Durera o lidské proporci byly pravděpodobně nejranější práce na výpočetní anatomii. Úsilí Noama Chomského v jeho průkopnictví počítačové lingvistiky inspirovalo původní formulaci výpočetní anatomie jako generativního modelu tvaru a formy z příkladů, na které se působilo prostřednictvím transformací.

Vzhledem k dostupnosti hustých 3D měření prostřednictvím technologií, jako je zobrazování magnetickou rezonancí (MRI), se výpočetní anatomie ukázala jako podoblast lékařského zobrazování a bioinženýrství pro extrakci anatomických souřadnicových systémů v měřítku morfomu ve 3D. Podstata této disciplíny sdílí silné překrývání s oblastmi, jako jsou počítačové vidění a kinematiky z tuhých těles , kde jsou předměty studovány analýzou skupiny odpovědné za pohyb v pochybnost. Výpočetní anatomie se odchyluje od počítačového vidění se zaměřením na rigidní pohyby, protože skupina nekonečně dimenzionálních diffeomorfismů je ústředním bodem analýzy biologických tvarů. Jedná se o pobočku školy pro analýzu obrazu a teorii vzorů na Brownově univerzitě, kterou propagoval Ulf Grenander . V Grenanderově obecné teorii metrických vzorů je vytváření prostorů vzorů do metrického prostoru jednou ze základních operací, protože schopnost shlukovat a rozpoznávat anatomické konfigurace často vyžaduje metriku blízkých a vzdálených tvarů. Diffeomorphometry metrický opatření Computational anatomie, jak daleko dvě diffeomorphic změny souřadnic jsou od sebe navzájem, což zase vyvolává metrický na tvarech a obrazy indexovaných k nim. Modely teorie metrických vzorů, zejména skupinová akce na oběžné dráze tvarů a forem, je ústředním nástrojem formálních definic ve výpočetní anatomii.

Dějiny

Výpočetní anatomie je studium tvaru a formulář na morphome nebo hrubé anatomie milimetru nebo morfologie měřítku, zaměřené na studium dílčích potrubí z bodů křivky ploch a subvolumes lidské anatomie. Časný moderní výpočetní neuroanatom byl David Van Essen, který prováděl některé z raných fyzických vývojů lidského mozku na základě tisku lidské kůry a řezání. Jean Talairach je zveřejnění Talairach souřadnic je důležitým mezníkem v morphome měřítku dokazuje fundamentální základ lokálních souřadných systémů pro studium neuroanatomie a tedy jasnou vazbu na grafech diferenciální geometrie . Souběžně s virtuálním mapováním ve výpočetní anatomii napříč hustými obrazovými souřadnicemi s vysokým rozlišením již došlo v nejranějším vývoji Ruzeny Bajcyové a Freda Booksteina na základě počítačové axiální tomografie a snímků magnetické rezonance . Nejdříve zavedení použití toků diffeomorphismů pro transformaci souřadnicových systémů v obrazové analýze a lékařském zobrazování provedli Christensen, Joshi, Miller a Rabbitt. ${\ displaystyle {\ mathbb {R}}^{3},}$

První formalizace výpočetní anatomie jako oběžné dráhy vzorových šablon v rámci skupinové akce diffeomorfismu byla v původní přednášce Grenandera a Millera s tímto názvem v květnu 1997 při 50. výročí divize aplikované matematiky na Brownově univerzitě a následné publikaci. To byl základ pro silný odklon od většiny předchozích prací o pokročilých metodách pro prostorovou normalizaci a registraci obrazu, které byly historicky postaveny na pojmech sčítání a rozšiřování základen. Struktura zachovávající transformace, která je ústředním bodem moderní oblasti výpočetní anatomie, homeomorfismy a diffeomorphismy, hladce nesou hladké podřazené potrubí. Jsou generovány pomocí Lagrangeových a Eulerových toků, které splňují zákon složení funkcí tvořících vlastnost skupiny, ale nejsou aditivní.

Původní model výpočetní anatomie byl trojnásobek, skupina , oběžná dráha tvarů a forem a zákony pravděpodobnosti, které kódují variace objektů na oběžné dráze. Šablona nebo kolekce šablon jsou prvky na oběžné dráze tvarů. ${\ displaystyle ({\ mathcal {G}}, {\ mathcal {M}}, {\ mathcal {P}}) \,}$${\ displaystyle g \ v {\ mathcal {G}}}$${\ displaystyle m \ v {\ mathcal {M}}}$${\ displaystyle P}$${\ Displaystyle m _ {\ mathrm {temp}} \ v {\ mathcal {M}}}$

Lagrangeovské a hamiltonovské formulace pohybových rovnic výpočetní anatomie se rozjely po roce 1997 s několika klíčovými setkáními, včetně setkání Luminy z roku 1997 pořádaného školou Azencott na Ecole-Normale Cachan na téma „Matematika rozpoznávání tvarů“ a Trimestre 1998 v Institutu Henri Poincar organizovaný Davidem Mumfordem „Otázky Mathématiques en Traitement du Signal et de l'Image“, které katalyzovaly skupiny Hopkins-Brown-ENS Cachan a následný vývoj a propojení výpočetní anatomie s vývojem v globální analýze.

Vývoj v oblasti výpočetní anatomie zahrnoval stanovení podmínek Sobelevovy hladkosti na metrice diffeomorfometrie, aby byla zajištěna existence řešení variačních problémů v prostoru diffeomorphismů, odvození Euler-Lagrangeových rovnic charakterizujících geodetiku prostřednictvím skupiny a souvisejících zákonů zachování, demonstrace metrických vlastností správné invariantní metriky, demonstrace, že Euler-Lagrangeovy rovnice mají dobře představovaný problém počáteční hodnoty s unikátními řešeními pro všechny časy a s prvními výsledky řezů křivek pro metriku diffeomorfometrie v orientačních prostorech. V návaznosti na jednání Los Alamos v roce 2002, Joshi původní velká deformace singulární Landmark řešení v oblasti výpočetní anatomii byly připojeny k vyvrcholila solitonů nebo Peakons jako řešení pro Camassa-Holm rovnice. Následně byla vytvořena spojení mezi Euler-Lagrangeovými rovnicemi výpočetní anatomie pro hustoty hybnosti pro pravo invariantní metriku uspokojující Sobolevovu plynulost k charakterizaci Eulerovy rovnice pro nestlačitelné toky Vladimírem Arnoldem, která popisuje geodetiku ve skupině objemů zachovávajících diffeomorfismy. Následovaly první algoritmy, obecně nazývané LDDMM pro velké deformační diffeomorfní mapování pro výpočet spojení mezi orientačními body v objemech a sférických potrubích, křivkách, proudech a plochách, objemech, tenzorech, varifoldech a časových řadách.

Tyto příspěvky výpočetní anatomie ke globální analýze spojené s nekonečně rozměrnými varietami podskupin skupiny diffeomorfismu nejsou zdaleka triviální. Původní myšlenka dělat diferenciální geometrie, zakřivení a geodesics na nekonečných varietách sahá až Bernhard Riemann ‚s Habilitation (über die Hypothesen, welche der Geometrie zu Grunde Liegen); klíčová moderní kniha, která položila základy takových myšlenek v globální analýze, pochází od Michora.

Aplikace v lékařském zobrazování výpočetní anatomie pokračovaly v rozkvětu po dvou organizovaných setkáních na konferencích Institute for Pure and Applied Mathematics na University of California, Los Angeles . Výpočetní anatomie byla užitečná při vytváření přesných modelů atrofie lidského mozku v morfomovém měřítku, stejně jako srdečních šablon, stejně jako při modelování biologických systémů. Od konce devadesátých let se výpočetní anatomie stala důležitou součástí vývoje nových technologií v oblasti lékařského zobrazování. Digitální atlasy jsou základní součástí moderního zdravotnického vzdělávání a výzkumu neuroimagingu v měřítku morfomů. Atlasové metody a virtuální učebnice, které pojímají variace jako u deformovatelných šablon, jsou středem mnoha platforem pro analýzu neuroobrazů, včetně Freesurfer, FSL, MRIStudio, SPM. Diffeomorfní registrace, zavedená v devadesátých letech, je nyní důležitým hráčem se stávajícími základnami kódů organizovanými kolem ANTS, DARTEL, DEMONS, LDDMM, StationaryLDDMM, FastLDDMM, jsou příklady aktivně používaných výpočetních kódů pro konstrukci korespondence mezi souřadnicovými systémy založenými na řídkých funkcích a hustých snímky. Morfometrie založená na Voxelu je důležitou technologií postavenou na mnoha z těchto principů.

Deformovatelný model oběžné dráhy výpočetní anatomie

Model lidské anatomie je deformovatelná šablona, ​​oběžná dráha příkladů v rámci skupinové akce. Deformovatelné modely šablon byly ústředním bodem Grenanderovy teorie metrických vzorů, účtování typičnosti pomocí šablon a účtování variability prostřednictvím transformace šablony. Dráha pod skupinovou akcí jako reprezentace deformovatelné šablony je klasická formulace z diferenciální geometrie. Prostor tvarů je označen , přičemž skupina má zákon složení ; označuje se působení skupiny na tvary , kde je působení skupiny definováno k uspokojení ${\ displaystyle m \ v {\ mathcal {M}}}$ ${\ displaystyle ({\ mathcal {G}}, \ circ)}$${\ displaystyle \ circ}$${\ Displaystyle g \ cdot m}$${\ Displaystyle g \ cdot m \ in {\ mathcal {M}}, m \ in {\ mathcal {M}}}$

${\ Displaystyle (g \ circ g^{\ prime}) \ cdot m = g \ cdot (g^{\ prime} \ cdot m) \ in {\ mathcal {M}}.}$

Oběžná dráha šablony se stává prostorem všech tvarů , přičemž je homogenní působením prvků . ${\ displaystyle {\ mathcal {M}}}$${\ Displaystyle {\ mathcal {M}} \ doteq \ {m = g \ cdot m _ {\ mathrm {temp}}, g \ in {\ mathcal {G}} \}}$${\ displaystyle {\ mathcal {G}}}$

Orbitální model výpočetní anatomie je abstraktní algebra - pro srovnání s lineární algebrou - protože skupiny působí na tvary nelineárně. Jedná se o zobecnění klasických modelů lineární algebry, ve kterých je sada konečných rozměrových vektorů nahrazena konečnými dimenzionálními anatomickými dílčími řadami (body, křivky, povrchy a objemy) a jejich obrazy a matice lineární algebry jsou nahrazeny transformacemi souřadnic založenými na lineárních a afinních skupinách a obecnějších vysoce dimenzionálních skupinách diffeomorfismu. ${\ displaystyle {\ mathbb {R}}^{n}}$${\ displaystyle n \ times n}$

Tvary a formy

Centrálními objekty jsou tvary nebo formy ve výpočetní anatomii, jednou sadou příkladů jsou 0,1,2,3-dimenzionální dílčí rozdělovače , druhou sadou příkladů jsou obrazy generované lékařským zobrazováním, jako je zobrazování pomocí magnetické rezonance (MRI) a funkční magnetická rezonance .${\ displaystyle {\ mathbb {R}}^{3}}$

0-rozměrné rozdělovače jsou orientační body nebo referenční body; 1-rozměrné potrubí jsou křivky, jako jsou sulcul a gyral křivky v mozku; 2-dimenzionální potrubí odpovídá hranicím substruktur v anatomii, jako jsou subkortikální struktury středního mozku nebo gyrální povrch neokortexu ; subobjemy odpovídají podoblastím lidského těla, srdce , thalamu , ledviny.

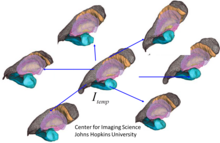
Orientační body jsou sbírka bodů bez jiné struktury, která vymezuje důležité referenční body v lidském tvaru a formě (viz související orientační obrázek). Sub potrubí tvary, jako jsou povrchy jsou kolekce bodů modelované jako parametrized lokální grafu nebo ponoření , (viz obrázek znázorňující tvary jako mesh plochy). Obrázky, jako jsou MR snímky nebo DTI obrázky , a jsou hustými funkcemi, jsou skaláry, vektory a matice (viz obrázek ukazující skalární obraz). ${\ Displaystyle X \ doteq \ {x_ {1}, \ dots, x_ {n} \} \ subset {\ mathbb {R}}^{3} \ in {\ mathcal {M}}}$${\ Displaystyle X \ subset {\ mathbb {R}}^{3} \ in {\ mathcal {M}}}$ ${\ Displaystyle m: U \ subset {\ mathbb {R}}^{1,2} \ rightarrow {\ mathbb {R}}^{3}}$${\ Displaystyle m (u), u \ v U}$${\ displaystyle I \ in {\ mathcal {M}}}$${\ Displaystyle I (x), x \ v X \ podmnožina {\ mathbb {R}}^{1,2,3}}$

Skupiny a skupinové akce

Skupiny a skupinové akce jsou inženýrské komunitě známé z univerzální popularizace a standardizace lineární algebry jako základního modelu pro analýzu signálů a systémů ve strojírenství , elektrotechnice a aplikované matematice . V lineární algebry matrice skupiny (matice s inverzí), jsou středové struktury, s působením skupiny vymezené podle obvyklé definice jako matice, působící na jako vektory; oběžná dráha v lineární algebře je množina -vektorů daných , což je skupinové působení matic po oběžné dráze . ${\ displaystyle A}$${\ displaystyle n \ times n}$${\ displaystyle x \ in {\ mathbb {R}}^{n}}$${\ displaystyle n \ times 1}$${\ displaystyle n}$${\ Displaystyle y = A \ cdot x \ in {\ mathbb {R}}^{n}}$${\ displaystyle {\ mathbb {R}}^{n}}$

Ústřední skupinou ve výpočetní anatomii definované na svazcích jsou diffeomorfismy, které jsou zobrazeními 3-složek , zákona o složení funkcí , s inverzními . ${\ displaystyle {\ mathbb {R}}^{3}}$ ${\ displaystyle {\ mathcal {G}} \ doteq Diff}$${\ Displaystyle \ phi (\ cdot) = (\ phi _ {1} (\ cdot), \ phi _ {2} (\ cdot), \ phi _ {3} (\ cdot))}$${\ Displaystyle \ phi \ circ \ phi ^{\ prime} (\ cdot) \ doteq \ phi (\ phi ^{\ prime} (\ cdot))}$${\ Displaystyle \ phi \ circ \ phi ^{-1} (\ cdot) = \ phi (\ phi ^{-1} (\ cdot)) = id}$

Nejoblíbenější jsou skalární obrázky, s akcí napravo pomocí inverze. ${\ Displaystyle I (x), x \ in {\ mathbb {R}}^{3}}$

${\ Displaystyle \ phi \ cdot I (x) = I \ circ \ phi ^{-1} (x), x \ in {\ mathbb {R}} ^{3}}$.

U dílčích rozdělovačů , parametrizovaných grafem nebo ponořením , působí diafeomorfní tok polohy ${\ Displaystyle X \ subset {\ mathbb {R}}^{3} \ in {\ mathcal {M}}}$ ${\ Displaystyle m (u), u \ v U}$

${\ Displaystyle \ phi \ cdot m (u) \ doteq \ phi \ circle m (u), u \ v U}$.

Bylo definováno několik skupinových akcí ve výpočetní anatomii .

Lagrangian a Eulerian toky pro generování diffeomorphismů

Pro studium kinematiky tuhých těles byly středem zájmu nízko dimenzionální matice Lieových skupin . Skupiny matic jsou nízko dimenzionální mapování, což jsou diffeomorfismy, které poskytují vzájemné korespondence mezi souřadnicovými systémy s hladkou inverzí. Matrice skupina rotací a stupnice mohou být generovány pomocí uzavřený tvar konečných trojrozměrné matrice, které jsou řešení jednoduchých obyčejných diferenciálních rovnic s řešeními daných exponenciální matice.

Pro studium deformovatelných tvarů ve výpočetní anatomii byla obecnější skupinou diffeomorfismu skupina volby, která je nekonečně dimenzionálním analogem. Vysoce dimenzionální skupiny difereomorfismu používané ve výpočetní anatomii jsou generovány prostřednictvím hladkých toků, které splňují Lagrangeovu a Eulerianovu specifikaci tokových polí, jak byla poprvé zavedena v., Která splňuje běžnou diferenciální rovnici:${\ Displaystyle \ phi _ {t}, t \ in [0,1]}$

${\ Displaystyle {\ frac {d} {dt}} \ phi _ {t} = v_ {t} \ circ \ phi _ {t}, \ \ phi _ {0} = id \;}$

( Lagrangeův tok )

s vektorových polí nazývaný Eulerian rychlost částic v poloze průtoku. Vektorová pole jsou funkce ve funkčním prostoru, modelovaném jako hladký Hilbertův prostor o vysoké dimenzi, přičemž jakobián proudění je také vysoce dimenzionální pole ve funkčním prostoru, spíše než nízko dimenzionální matice jako v matici skupiny. Toky byly poprvé zavedeny pro velké deformace v přizpůsobování obrazu; je okamžitá rychlost částic v čase . ${\ Displaystyle v \ doteq (v_ {1}, v_ {2}, v_ {3})}$${\ displaystyle {\ mathbb {R}}^{3}}$${\ displaystyle \ phi}$${\ displaystyle \ D \ phi \ doteq ({\ frac {\ částečné \ phi _ {i}} {\ částečné x_ {j}}})}$${\ displaystyle {\ dot {\ phi}} _ {t} (x)}$${\ displaystyle x}$${\ displaystyle t}$

Inverze požadovaná pro skupinu je definována na eulerovském vektorovém poli s advektivním inverzním tokem ${\ Displaystyle \ phi _ {t}^{-1}, t \ v [0,1]}$

${\ Displaystyle {\ frac {d} {dt}} \ phi _ {t}^{-1} =-(D \ phi _ {t}^{-1}) v_ {t}, \ \ phi _ { 0}^{-1} = id \.}$

( Inverzní dopravní tok )

Skupina diffeomorfismu výpočetní anatomie

Skupina diffeomorphismů je velmi velká. Aby se zajistily plynulé toky diffeomorphismů, které se vyhýbají šokovým řešením pro inverzní, vektorová pole musí být alespoň 1krát spojitě diferencovatelná v prostoru. U diffeomorphismů na jsou vektorová pole modelována jako prvky Hilbertovy prostoru pomocí Sobolevových vkládajících vět, takže každý prvek má striktně větší než 2 zobecněné prostorově derivovatelné integrovatelné čtverce (tedy je dostačující), čímž se získají jednorázové spojitě diferencovatelné funkce. ${\ displaystyle {\ mathbb {R}}^{3}}$${\ Displaystyle (V, \ | \ cdot \ | _ {V})}$${\ Displaystyle v_ {i} \ v H_ {0}^{3}, i = 1,2,3,}$

Skupina diffeomorfismu jsou toky s vektorovými poli absolutně integrovatelnými v Sobolevově normě:

${\ Displaystyle Diff_ {V} \ doteq \ {\ varphi = \ phi _ {1}: {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t}, \ phi _ {0} = id, \ int _ {0}^{1} \ | v_ {t} \ | _ {V} dt <\ infty \} \,}$

( Diffeomorphism Group )

kde s mapováním lineárního operátoru do duálního prostoru , s integrálem vypočítaným integrací po částech, když je zobecněnou funkcí v duálním prostoru. ${\ Displaystyle \ | v \ | _ {V}^{2} \ doteq \ int _ {X} Av \ cdot vdx, \ v \ in V \,}$${\ displaystyle A}$${\ Displaystyle A: V \ mapsto V^{*}}$${\ displaystyle Av \ in V^{*}}$

Diffeomorfometrie: metrický prostor tvarů a forem

Studium metrik na skupinách diffeomorphismů a studium metrik mezi varietami a povrchy bylo oblastí významného zkoumání. Metrika diffeomorfometrie měří, jak blízko a daleko od sebe jsou dva tvary nebo obrazy; metrická délka je nejkratší délka toku, který přenáší jeden souřadnicový systém do druhého.

Známá euklidovská metrika často není přímo použitelná, protože vzory tvarů a obrázků netvoří vektorový prostor. V Riemannovském orbitálním modelu výpočetní anatomie nepůsobí diffeomorfismy působící na formy lineárně. Existuje mnoho způsobů, jak definovat metriky, a pro sady přidružené k tvarům je Hausdorffova metrika další. Metoda, kterou používáme k indukci Riemannovy metriky, se používá k indukci metriky na oběžné dráze tvarů tím, že ji definujeme z hlediska metrické délky mezi transformacemi toků diffeomorfních souřadnicových systémů. Měření délek geodetického toku mezi souřadnicovými systémy na oběžné dráze tvarů se nazývá diffeomorfometrie . ${\ Displaystyle \ phi \ cdot m \ in {\ mathcal {M}}, \ phi \ in Diff_ {V}, m \ in {\ mathcal {M}}}$

Pravo invariantní metrika diffeomorfismů

Definujte vzdálenost na skupině diffeomorphismů

${\ Displaystyle d_ {Diff_ {V}} (\ psi, \ varphi) = \ inf _ {v_ {t}} \ left (\ int _ {0}^{1} \ int _ {X} Av_ {t} \ cdot v_ {t} dx \ dt: \ phi _ {0} = \ psi, \ phi _ {1} = \ varphi, {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t} \ right)^{1/2} \;}$

( metric-diffeomorphisms )

toto je pravo invariantní metrika diffeomorfometrie, neměnná k reparametrizaci prostoru, protože pro všechny , ${\ displaystyle \ phi \ in Diff_ {V}}$

${\ Displaystyle d_ {Diff_ {V}} (\ psi, \ varphi) = d_ {Diff_ {V}} (\ psi \ circ \ phi, \ varphi \ circ \ phi)}$.

Metrika tvarů a forem

Vzdálenost tvarů a forem , ${\ Displaystyle d _ {\ mathcal {M}}: {\ mathcal {M}} \ times {\ mathcal {M}} \ rightarrow \ mathbb {R} ^{+}}$

${\ displaystyle d _ {\ mathcal {M}} (m, n) = \ inf _ {\ phi \ in \ operatorname {Diff} _ {V}: \ phi \ cdot m = n} d _ {\ operatorname {Diff} _ {V}} (id, \ phi) \;}$

( metrické tvary-formy )

obrázky jsou označeny na oběžné dráze jako a metrické . ${\ displaystyle I \ v {\ mathcal {I}}}$${\ displaystyle, d _ {\ mathcal {I}}}$

Akční integrál pro Hamiltonův princip difeomorfních toků

V klasické mechanice evoluce fyzikálních systémů je popsáno řešení rovnice Euler-Lagrangeových spojeným s principem Least-action of Hamilton . Toto je standardní způsob, například získání Newtonových zákonů pohybu volných částic. Obecněji lze Euler-Lagrangeovy rovnice odvodit pro systémy generalizovaných souřadnic . Euler-Lagrangeova rovnice ve výpočetní anatomii popisuje geodetické nejkratší cesty mezi souřadnicovými systémy metriky diffeomorfismu. Ve výpočetní anatomii jsou generalizovanými souřadnicemi tok diffeomorfismu a jeho Lagrangeova rychlost , dva související prostřednictvím eulerovské rychlosti . Hamiltonův princip pro generování Euler-Lagrangeovy rovnice vyžaduje akční integrál na Lagrangeově daném ${\ displaystyle \ phi, {\ dot {\ phi}}}$${\ Displaystyle v \ doteq {\ dot {\ phi}} \ circ \ phi ^{-1}}$

${\ Displaystyle J (\ phi) \ doteq \ int _ {0}^{1} L (\ phi _ {t}, {\ dot {\ phi}} _ {t}) dt \;}$

( Hamiltonian-Integrated-Lagrangian )

Lagrangian je dán kinetickou energií:

${\ Displaystyle L (\ phi _ {t}, {\ dot {\ phi}} _ {t}) \ doteq {\ frac {1} {2}} \ int _ {X} A ({\ dot {\ phi}} _ {t} \ circ \ phi _ {t}^{-1}) \ cdot ({\ dot {\ phi}} _ {t} \ circ \ phi _ {t}^{-1}) dx = {\ frac {1} {2}} \ int _ {X} Av_ {t} \ cdot v_ {t} \ dx \.}$

( Lagrangian-Kinetic-Energy )

Dynomomorfní nebo eulerovský tvar hybnosti

Ve výpočetní anatomii byl nejprve nazýván eulerovským nebo diffeomorfním tvarem hybnosti, protože když byl integrován proti eulerovské rychlosti, dává hustotu energie a protože existuje zachování hybnosti tvarů odlišných tvarů, které platí. Operátor je zobecněný moment setrvačnosti nebo setrvačný operátor. ${\ displaystyle Av}$${\ displaystyle v}$${\ displaystyle A}$

Euler -Lagrangeova rovnice o hybnosti tvaru pro geodetiku na skupině diffeomorphismů

Klasický výpočet Euler-Lagrangeovy rovnice z Hamiltonova principu vyžaduje poruchu Lagrangeova na vektorovém poli v kinetické energii s ohledem na poruchu toku prvního řádu. To vyžaduje úpravu Lieovou závorkou vektorového pole , danou operátorem, který zahrnuje jakobiány dané ${\ displaystyle ad_ {v}: w \ in V \ mapsto V}$

${\ Displaystyle ad_ {v} [w] \ doteq [v, w] \ doteq (Dv) w- (Dw) v \ in V}$.

Definování adjoint pak variace prvního řádu dává hybnost Eulerianova tvaru uspokojující zobecněnou rovnici: ${\ displaystyle ad_ {v}^{*}: V^{*} \ rightarrow V^{*},}$${\ displaystyle Av \ in V^{*}}$

${\ displaystyle {\ frac {d} {dt}} Av_ {t}+ad_ {v_ {t}}^{*} (Av_ {t}) = 0 \, \ t \ in [0,1] \; }$

( EL-General )

význam pro všechny hladké ${\ Displaystyle w \ v V,}$

${\ displaystyle \ int _ {X} \ left ({\ frac {d} {dt}} Av_ {t}+ad_ {v_ {t}}^{*} (Av_ {t}) \ right) \ cdot wdx = \ int _ {X} {\ frac {d} {dt}} Av_ {t} \ cdot wdx+\ int _ {X} Av_ {t} \ cdot ((Dv_ {t}) w- (Dw) v_ { t}) dx = 0.}$

Výpočetní anatomie je studium pohybů dílčích potrubí, bodů, křivek, ploch a objemů. Hybnost spojená s body, křivkami a povrchy jsou singulární, což znamená, že hybnost je soustředěna na podmnožiny, jejichž rozměry jsou v Lebesgueově měřítku . V takových případech je energie stále dobře definována, protože ačkoli jde o zobecněnou funkci, vektorová pole jsou hladká a eulerovská hybnost je chápána prostřednictvím jejího působení na hladké funkce. Dokonalou ukázkou toho je, že i když jde o superpozici delta-diraců, rychlost souřadnic v celém objemu se pohybuje plynule. Rovnice Euler-Lagrange ( EL-General ) o diffeomorfismech pro generalizované funkce byla odvozena v. V Riemannově metrické a Lie-Bracketově interpretaci Euler-Lagrangeovy rovnice na geodetické derivace jsou poskytovány termíny jako pomocný operátor a Lieova závorka pro skupina diffeomorphismů. Začalo se tomu říkat rovnice EPDiff pro diffeomorfismy připojující se k Eulerově-Poincareově metodě, která byla studována v kontextu setrvačného operátoru pro nestlačitelné tekutiny bez divergence. ${\ displaystyle {\ mathbb {R}}^{3}}$${\ displaystyle \ leq 2}$${\ displaystyle (Av_ {t} \ mid v_ {t})}$${\ displaystyle Av_ {t}}$${\ displaystyle Av \ in V^{*}}$${\ displaystyle A = identita}$

Dynamiomorfní tvar hybnosti: klasická vektorová funkce

Pro případ hustoty hybnosti má potom Eulerova -Lagrangeova rovnice klasické řešení:${\ Displaystyle (Av_ {t} \ mid w) = \ int _ {X} \ mu _ {t} \ cdot w \, dx}$

${\ Displaystyle {\ frac {d} {dt}} \ mu _ {t}+(Dv_ {t})^{T} \ mu _ {t}+(D \ mu _ {t}) v_ {t} +(\ nabla \ cdot v) \ mu _ {t} = 0 \, t \ v [0,1].}$

( EL-Classic )

Euler-Lagrangeova rovnice o diffeomorfismech, klasicky definovaná pro hustoty hybnosti, se poprvé objevila v lékařské analýze obrazu.

Riemannian exponenciální (geodetické umístění) a Riemannian logaritmus (geodetické souřadnice)

V lékařském zobrazování a výpočetní anatomii jsou polohování a koordinace tvarů základními operacemi; systém pro určování polohy anatomických souřadnic a tvarů postavený na metrice a Euler-Lagrangeově rovnici geodetický polohovací systém, který byl poprvé vysvětlen v Miller Trouve a Younes. Řešení geodetiky z počátečních podmínek se nazývá Riemannian-exponenciální, mapování identity skupiny. ${\ displaystyle v_ {0}}$${\ displaystyle Exp _ {\ rm {id}} (\ cdot): V \ to Diff_ {V}}$

Riemannianova exponenciála splňuje počáteční podmínky , dynamiku vektorového pole , ${\ displaystyle Exp_ {id} (v_ {0}) = \ phi _ {1}}$${\ displaystyle {\ dot {\ phi}} _ {0} = v_ {0}}$${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ circle \ phi _ {t}, t \ v [0,1]}$

• pro klasickou rovnice diffeomorphic tvar hybnost , a pak${\ displaystyle \ int _ {X} Av_ {t} \ cdot w \, dx}$${\ displaystyle Av \ in V}$

${\ Displaystyle \ \ \ \ \ frac {d} {dt}} Av_ {t}+(Dv_ {t})^{T} Av_ {t}+(DAv_ {t}) v_ {t}+(\ nabla \ cdot v) Av_ {t} = 0 \;}$

• pro všeobecné rovnice, pak , ,${\ displaystyle Av \ in V^{*}}$${\ Displaystyle w \ v V}$

${\ Displaystyle \ \ \ \ int _ {X} {\ frac {d} {dt}} Av_ {t} \ cdot wdx+\ int _ {X} Av_ {t} \ cdot ((Dv_ {t}) w- (Dw) v_ {t}) dx = 0.}$

Výpočet toku na souřadnice Riemannův logaritmus , mapování identity z vektorového pole ; ${\ displaystyle v_ {0}}$${\ displaystyle Log _ {\ rm {id}} (\ cdot): Diff_ {V} \ to V}$${\ Displaystyle \ varphi}$${\ displaystyle v_ {0} \ v V}$

${\ Displaystyle Log_ {id} (\ varphi) = v_ {0} \ {\ text {počáteční stav EL geodesic}} {\ dot {\ phi}} _ {0} = v_ {0}, \ phi _ { 0} = id, \ phi _ {1} = \ varphi \.}$

Rozšířena na celou skupinu, kterou se stali

${\ Displaystyle \ phi = Exp _ {\ varphi} (v_ {0} \ circle \ varphi) \ doteq Exp_ {id} (v_ {0}) \ circ \ varphi}$ ; . ${\ Displaystyle Log _ {\ varphi} (\ phi) \ doteq Log_ {id} (\ phi \ circ \ varphi ^{-1}) \ circ \ varphi}$

Jedná se o vzájemné inverze pro jedinečná řešení Logarithmu; první se nazývá geodetické určování polohy, druhý geodetické souřadnice (viz Exponenciální mapa, riemannianská geometrie pro konečnou dimenzionální verzi). Geodetická metrika je lokální zploštění riemannianského souřadného systému (viz obrázek).

Hamiltonovská formulace výpočetní anatomie

Ve výpočetní anatomii se diffeomorfismy používají k tlačení souřadnicových systémů a vektorová pole se používají jako kontrola v rámci anatomické orbity nebo morfologického prostoru. Model je to dynamický systém, tok souřadnic a řídicí vektorové pole spojené přes hamiltoniánem pohledu reparameterizes rozložení hybnosti , pokud jde o hybnosti konjugátu nebo kanonické hybnosti , i ntroduced jako Lagrangeova multiplikátoru omezovat Lagrangeovy rychlost .accordingly : ${\ displaystyle t \ mapsto \ phi _ {t} \ in \ operatorname {Diff} _ {V}}$${\ Displaystyle t \ mapsto v_ {t} \ v V}$${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ cdot \ phi _ {t}, \ phi _ {0} = id.}$${\ displaystyle Av \ in V^{*}}$ ${\ displaystyle p: {\ dot {\ phi}} \ mapsto (p \ mid {\ dot {\ phi}})}$${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t}}$

${\ Displaystyle H (\ phi _ {t}, p_ {t}, v_ {t}) = \ int _ {X} p_ {t} \ cdot (v_ {t} \ circ \ phi _ {t}) dx -{\ frac {1} {2}} \ int _ {X} Av_ {t} \ cdot v_ {t} dx.}$

Tato funkce je rozšířený hamiltonián. Princip Pontryaginova maxima poskytuje optimalizační vektorové pole, které určuje uspokojivý geodetický tok i redukovaný hamiltonián ${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ circle \ phi _ {t}, \ phi _ {0} = id,}$

${\ Displaystyle H (\ phi _ {t}, p_ {t}) \ doteq \ max _ {v} H (\ phi _ {t}, p_ {t}, v) \.}$

Lagrangeův multiplikátor ve své činnosti jako lineární forma má svůj vlastní vnitřní součin kanonické hybnosti působící na rychlost toku, která je závislá na tvaru, např. Pro orientační body součet, pro povrchy povrchový integrál a. u svazků je to objem integrál s ohledem na na . Ve všech případech mají jádra Zelených váhy, které jsou kanonickou hybností vyvíjející se podle běžné diferenciální rovnice, která odpovídá EL, ale je geodetickou reparametrizací v kanonické hybnosti. Optimalizační vektorové pole je dáno vztahem ${\ displaystyle dx}$${\ displaystyle {\ mathbb {R}}^{3}}$

${\ Displaystyle v_ {t} \ doteq \ arg max_ {v} H (\ phi _ {t}, p_ {t}, v)}$

s dynamikou kanonické hybnosti reparametrizující vektorové pole podél geodetického

${\ Displaystyle {\ begin {cases} {\ dot {\ phi}} _ {t} = {\ frac {\ částečná H (\ phi _ {t}, p_ {t})} {\ částečná p}} \ \ {\ dot {p}} _ {t} =-{\ frac {\ částečné H (\ phi _ {t}, p_ {t})} {\ částečné \ phi}} \\\ end {případy}} }$

( Hamiltonian-Dynamics )

Stacionarita hamiltonovské a kinetické energie podél Euler -Lagrange

Zatímco vektorová pole jsou rozšířena po celém prostoru pozadí , geodetické toky spojené s dílčími rozdělovači mají hybnost eulerovského tvaru, která se vyvíjí jako zobecněná funkce soustředěná do podrozdělovačů. Pro orientační body má geodetika hybnost eulerovského tvaru, což je superpozice distribucí delta cestujících s konečným počtem částic; diffeomorfní tok souřadnic má rychlosti v rozsahu vážených Greenových jader. U povrchů je hybnost povrchový integrál delta distribucí cestujících s povrchem. ${\ displaystyle {\ mathbb {R}}^{3}}$${\ displaystyle Av_ {t} \ v V^{*}}$

Geodetika spojující souřadnicové systémy splňující EL-General mají stacionaritu Lagrangian. Hamiltonian je dán extrémem podél cesty , který se rovná Lagrangian-Kinetic-Energy a je nehybný podél EL-General . Definování geodetické rychlosti na identitě , pak podél geodetické ${\ Displaystyle t \ v [0,1]}$${\ Displaystyle H (\ phi, p) = \ max _ {v} H (\ phi, p, v)}$${\ Displaystyle v_ {0} = \ arg \ max _ {v} H (\ phi _ {0}, p_ {0}, v)}$

${\ Displaystyle H (\ phi _ {t}, p_ {t}) = H (\ phi _ {0}, p_ {0}) = {\ frac {1} {2}} \ int _ {X} p_ {0} \ cdot v_ {0} dx = {\ frac {1} {2}} \ int _ {X} Av_ {0} \ cdot v_ {0} dx = {\ frac {1} {2}} \ int _ {X} Av_ {t} \ cdot v_ {t} dx}$

( Hamiltonian-Geodesics )

Stacionarita Hamiltoniána ukazuje výklad Lagrangeova multiplikátoru jako hybnosti; integrovaný proti rychlosti dává hustotu energie. Kanonická hybnost má mnoho jmen. Při optimální kontrole jsou toky interpretovány jako stav a jsou interpretovány jako konjugovaný stav nebo sdružená hybnost. Geodézie EL implikují specifikaci vektorových polí nebo eulerovskou hybnost při nebo specifikaci kanonické hybnosti určuje tok. ${\ displaystyle {\ dot {\ phi}}}$${\ displaystyle \ phi}$${\ displaystyle p}$${\ displaystyle v_ {0}}$${\ displaystyle Av_ {0}}$${\ displaystyle t = 0}$${\ displaystyle p_ {0}}$

Metrika geodetických toků orientačních bodů, povrchů a objemů na oběžné dráze

Ve výpočetní anatomii jsou podrozdělovači body, křivky, povrchy a dílčí objemy, které jsou základními primitivy. Geodetické toky mezi dílčími rozdělovači určují vzdálenost a tvoří základní měřicí a transportní nástroje diffeomorfometrie . V geodetice má vektorové pole určené konjugovanou hybností a Greenovým jádrem setrvačného operátoru definujícím eulerovskou hybnost . Metrická vzdálenost mezi souřadnicovými systémy spojenými geodeticky určenou indukovanou vzdáleností mezi identitou a skupinovým prvkem: ${\ displaystyle t = 0}$${\ displaystyle v_ {0} = Kp_ {0}}$${\ displaystyle K = A^{-1}}$

${\ Displaystyle d_ {Diff_ {V}} (id, \ varphi) = \ | Log_ {id} (\ varphi) \ | _ {V} = \ | v_ {0} \ | _ {V} = {\ sqrt {2H (id, p_ {0})}}}$

Zákony zachování hybnosti tvarů odlišných tvarů pro výpočetní anatomii

Vzhledem k nejmenší akci existuje přirozená definice hybnosti spojená s generalizovanými souřadnicemi; množství působící proti rychlosti dává energii. Pole studovalo dvě formy, hybnost spojenou s eulerovským vektorovým polem nazývaným eulerovský hybnost diffeomorfního tvaru a hybnost spojenou s počátečními souřadnicemi nebo kanonickými souřadnicemi nazývanými hybnost kanonického diffeomorfního tvaru . Každý má zákon o zachování. Zachování hybnosti jde ruku v ruce s generálem EL . Ve výpočetní anatomii je Eulerian Momentum, protože když je integrován proti Eulerian rychlosti, dává hustotu energie; operátor generalizovaný moment setrvačnosti nebo setrvačný operátor, který působí na eulerovskou rychlost, dává hybnost, která je zachována podél geodetiky:${\ displaystyle Av}$${\ displaystyle v}$${\ displaystyle A}$

${\ Displaystyle {\ begin {matrix} {\ text {Eulerian}} & \ \ \ \ \ \ frac {d} {dt}} \ int _ {X} Av_ {t} \ cdot ((D \ phi _ { t}) w) \ circ \ phi _ {t}^{-1}) dx = 0 \, \ t \ v [0,1]. \\ & \\ {\ text {Canonical}} & \ \ \ \ \ \ \ \ \ \ \ \ \ frac {d} {dt}} \ int _ {X} p_ {t} \ cdot ((D \ phi _ {t}) w) dx = 0 \, \ t \ v [0,1] \ {\ text {pro všechny}} \ w \ ve V \. \ end {matrix}}}$

( Euler-Conservation-Constant-Energy )

Zachování hybnosti tvaru Eulerian bylo ukázáno a vyplývá z EL-General ; zachování kanonické hybnosti bylo ukázáno v

Geodetická interpolace informací mezi souřadnicovými systémy prostřednictvím variačních problémů

Konstrukce diffeomorfních korespondencí mezi tvary vypočítá počáteční souřadnice vektorového pole a související váhy na Zelených jádrech . Tyto počáteční souřadnice jsou určeny shodou tvarů, které se nazývají velké deformační diffeomorfní metrické mapování (LDDMM) . LDDMM byl vyřešen pro orientační body s korespondencí i bez ní a pro husté porovnávání obrázků. křivky, povrchy, husté vektorové a tenzorové snímky a varifoldy, které odstraňují orientaci. LDDMM vypočítává geodetické toky EL-General na cílové souřadnice, přičemž k akčnímu integrálu přidává podmínku shody koncového bodu měřící shodu prvků na oběžné dráze v rámci transformace souřadnicového systému. Existence řešení byla zkoumána kvůli shodě obrázků. Řešení variačních problémů uspokojí EL generální za pomocí okrajových podmínek. ${\ displaystyle v_ {0} \ v V}$${\ displaystyle p_ {0}}$${\ displaystyle {\ frac {1} {2}} \ int _ {0}^{1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt}$${\ Displaystyle E: \ phi _ {1} \ rightarrow R^{+}}$${\ Displaystyle t \ v [0,1)}$

Shoda založená na minimalizaci akce kinetické energie s podmínkou koncového bodu

${\ Displaystyle {\ text {min}} _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^{-1}, \ phi _ {0} = id} C (\ phi) \ doteq {\ frac {1} {2}} \ int _ {0}^{1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt+E (\ phi _ {1})}$

${\ Displaystyle {\ begin {cases} {\ text {Euler Conservation}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ frac {d} {dt}} Av_ {t}+ad_ {v_ {t} }^{*} (Av_ {t}) = 0, \ t \ in [0,1) \, \\ {\ text {Boundary Condition}} & \ \ \ \ phi _ {0} = id, Av_ { 1} =-{\ frac {\ částečné E (\ phi)} {\ částečné \ phi}} | _ {\ phi = \ phi _ {1}} \. \ End {případy}}}$

Zachování z EL-General rozšiřuje BC na zbytek cesty . Nepřesný problém shody s termínem shody koncového bodu má několik alternativních forem. Jednou z klíčových myšlenek stacionarity hamiltoniánů podél geodetického řešení je integrované snížení provozních nákladů na počáteční náklady při t = 0, geodetika EL-General je určena jejich počátečním stavem . ${\ displaystyle t = 1}$${\ Displaystyle t \ v [0,1)}$${\ Displaystyle E (\ phi _ {1})}$${\ displaystyle v_ {0}}$

Na provozní náklady se sníží na počáteční náklady určí z jádra Surf.-Land.-geodetik . ${\ displaystyle v_ {0} = Kp_ {0}}$

Shoda založená na geodetickém fotografování

${\ Displaystyle \ min _ {v_ {0}} C (v_ {0}) \ doteq {\ frac {1} {2}} \ int _ {X} Av_ {0} \ cdot v_ {0} dx+E (\ mathrm {Exp} _ {\ mathrm {id}} (v_ {0}) \ cdot I_ {0}) \;}$

${\ Displaystyle \ min _ {p_ {0}} C (p_ {0}) = {\ frac {1} {2}} \ int _ {X} p_ {0} \ cdot Kp_ {0} dx+E ( \ mathrm {Exp} _ {\ text {id}} (Kp_ {0}) \ cdot I_ {0})}$

Problém shody výslovně indexovaný na počáteční stav se nazývá střelba, kterou lze také reparamerizovat prostřednictvím konjugované hybnosti . ${\ displaystyle v_ {0}}$${\ displaystyle p_ {0}}$

Husté shody obrázků ve výpočetní anatomii

Husté přizpůsobování obrázků má nyní dlouhou historii, přičemž nejranější snahy využívají malou deformační strukturu. Velké deformace začaly na počátku devadesátých let, kdy byla založena první existence řešení variačního problému pro toky diffeomorphismů pro hustou shodu obrazu. Začněte řešit jedním z prvních algoritmů LDDMM založených na řešení variačního párování s koncovým bodem definovaným hustým snímky s ohledem na vektorová pole, přičemž variace na vektorová pole. Jiné řešení pro hustou shodu obrazu reparametrizuje problém optimalizace z hlediska stavu, který poskytuje řešení z hlediska nekonečně malého působení definovaného rovnicí advekce . ${\ Displaystyle q_ {t} \ doteq I \ circ \ phi _ {t}^{-1}, q_ {0} = I}$

Shoda hustého obrazu LDDMM

Pro Beg's LDDMM označte Image with group action . Když se na to díváme jako na optimální problém kontroly, stav systému je rozdvojný tok souřadnic , přičemž dynamika souvisí s řízením daným stavem . Podmínka shody koncového bodu dává variační problém ${\ Displaystyle I (x), x \ in X}$${\ Displaystyle \ phi \ cdot I \ doteq I \ circ \ phi ^{-1}}$${\ Displaystyle \ phi _ {t}, t \ in [0,1]}$${\ Displaystyle v_ {t}, t \ v [0,1]}$${\ displaystyle {\ dot {\ phi}} = v \ circ \ phi}$${\ Displaystyle E (\ phi _ {1}) \ doteq \ | I \ circle \ phi _ {1}^{-1} -I^{\ prime} \ |^{2}}$

${\ displaystyle {\ begin {matrix} & \ \ \ \ \ \ min _ {v: {\ dot {\ phi}} = v \ circle \ phi} C (v) \ doteq {\ frac {1} {2 }} \ int _ {0}^{1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt+{\ frac {1} {2}} \ int _ {{\ mathbb {R}} ^{3}} | I \ circ \ phi _ {1}^{-1} (x) -I^{\ prime} (x) |^{2} dx \ end {matrix}}}$

( Husté porovnávání obrázků )

${\ Displaystyle {\ begin {cases} & {\ text {Endpoint Condition:}} \ \ \ \ \ Av_ {1} = \ mu _ {1} dx, \ mu _ {1} = (I \ circ \ phi _ {1}^{-1} -I^{\ prime}) \ nabla (I \ circ \ phi _ {1}^{-1}) \, \\ & {\ text {Conservation:}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Av_ {t} = \ mu _ {t} \, dx, \ \ mu _ {t} = (D \ phi _ {t}^{-1} )^{T} \ mu _ {0} \ circ \ phi _ {t}^{-1} | D \ phi _ {t}^{-1} | \. \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ mu _ {0} = (II^{\ prime} \ circ \ phi _ {1}) \ nabla I | D \ phi _ {1} | \. \\\ end {cases}}}$

Begův iterativní algoritmus LDDMM má pevné body, které splňují nezbytné podmínky optimalizátoru. Iterační algoritmus je uveden v Begově algoritmu LDDMM pro shodu hustého obrazu .

Hamiltonian LDDMM v redukovaném advelovaném stavu

Označte Image se stavem a stavem a kontrolou souvisejícími s dynamikou danými advektivním termínem . Koncový bod uvádí variační problém ${\ Displaystyle I (x), x \ in X}$${\ Displaystyle q_ {t} \ doteq I \ circ \ phi _ {t}^{-1}}$ ${\ displaystyle {\ dot {q}} _ {t} =-\ nabla q_ {t} \ cdot v_ {t}}$${\ Displaystyle E (q_ {1}) \ doteq \ | q_ {1} -I^{\ prime} \ |^{2}}$

${\ Displaystyle {\ begin {matrix} & \ \ \ \ \ \ min _ {q: {\ dot {q}} = v \ circle q} C (v) \ doteq {\ frac {1} {2}} \ int _ {0}^{1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt+{\ frac {1} {2}} \ int _ {{\ mathbb {R}}^{ 3}} | q_ {1} (x) -I^{\ prime} (x) |^{2} dx \ end {matrix}}}$

( Husté porovnávání obrázků )

Viallardův iterativní hamiltonovský LDDMM má pevné body, které splňují nezbytné podmínky optimalizátoru.

Porovnání obrazu tenzoru difúze ve výpočetní anatomii

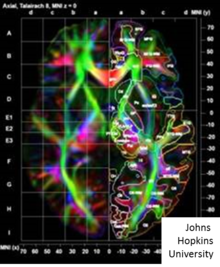
Hustá shoda tenzoru LDDMM bere obrázky jako 3x1 vektory a 3x3 tenzory řešící přizpůsobení variačních problémů mezi souřadnicovým systémem na základě základních vlastních vektorů obrazu MRI (DTI) difúzního tenzoru označeného sestávajícím z -tenzoru v každém voxelu. Několik skupinových akcí definovaných na základě Frobeniusovy maticové normy mezi čtvercovými maticemi . Na doprovodném obrázku je zobrazen obrázek DTI ilustrovaný prostřednictvím jeho barevné mapy zobrazující orientace vlastních vektorů matice DTI u každého voxelu s barvou určenou orientací směrů. Naznačovat tensor obraz s charakteristických prvků , . ${\ Displaystyle M (x), x \ in {\ mathbb {R}}^{3}}$${\ displaystyle 3 \ times 3}$${\ Displaystyle \ | A \ | _ {F}^{2} \ doteq traceA^{T} A}$${\ displaystyle 3 \ times 3}$${\ Displaystyle M (x), x \ in {\ mathbb {R}}^{3}}$${\ Displaystyle \ {\ lambda _ {i} (x), e_ {i} (x), i = 1,2,3 \}}$${\ Displaystyle \ lambda _ {1} \ geq \ lambda _ {2} \ geq \ lambda _ {3}}$

Transformace souřadnicového systému založená na zobrazování DTI využila dvou akcí, jedné založené na principu vlastního vektoru nebo celé matice .

Srovnání LDDMM na základě hlavního vlastního vektoru matice tenzoru difúze bere obraz jako pole jednotkových vektorů definovaných prvním vlastním vektorem. Skupinová akce se stává ${\ Displaystyle I (x), x \ in {\ mathbb {R}}^{3}}$

${\ Displaystyle \ varphi \ cdot I = {\ begin {cases} {\ frac {D _ {\ varphi ^{-1}} \ varphi I \ circle \ varphi ^{-1} \ | I \ circ \ varphi ^{ -1} \ |} {\ | D _ {\ varphi ^{-1}} \ varphi I \ circ \ varphi ^{-1} \ |}} & I \ circ \ varphi \ neq 0; \\ 0 & {\ text {jinak.}} \ end {cases}}}$

Shoda LDDMM na základě celé tenzorové matice má skupinovou akci a transformuje se na vlastní vektory ${\ Displaystyle \ varphi \ cdot M = (\ lambda _ {1} {\ hat {e}} _ {1} {\ hat {e}} _ {1}^{T}+\ lambda _ {2} { \ hat {e}} _ {2} {\ hat {e}} _ {2}^{T}+\ lambda _ {3} {\ hat {e}} _ {3} {\ hat {e}} _ {3} ^{T}) \ circ \ varphi ^{-1},}$

${\ Displaystyle {\ begin {aligned} {\ hat {e}} _ {1} & = {\ frac {D \ varphi e_ {1}} {\ | D \ varphi e_ {1} \ |}} \, \ \ \ \ \ hat {e}} _ {2} = {\ frac {D \ varphi e_ {2}-\ langle {\ hat {e}} _ {1}, D \ varphi e_ {2} \ rangle {\ hat {e}} _ {1}} {\ sqrt {\ | D \ varphi e_ {2} \ |^{2}-\ langle {\ hat {e}} _ {1}, D \ varphi e_ {2} \ rangle ^{2}}}} \, \ \ \ \ \ hat {e}} _ {3} = {\ hat {e}} _ {1} \ times {\ hat {e}} _ {2} \ end {aligned}}}$.

Variační problémová shoda na hlavní vlastní vektor nebo matici je popsána porovnáváním obrazu tenzoru LDDMM .

Difúzní obraz s vysokým úhlovým rozlišením (HARDI) ve výpočetní anatomii

Difúzní zobrazování s vysokým úhlovým rozlišením (HARDI) řeší dobře známé omezení DTI, to znamená, že DTI může v každém místě odhalit pouze jednu dominantní orientaci vláken. HARDI měří difúzi v rovnoměrně rozložených směrech na kouli a může charakterizovat složitější geometrie vláken. HARDI lze použít k rekonstrukci orientační distribuční funkce (ODF), která charakterizuje úhlový profil funkce hustoty difúzní hustoty molekul vody. ODF je funkce definovaná na jednotkové sféře . ${\ displaystyle n}$${\ displaystyle {\ mathbb {S}}^{2}}$

Hustá shoda LDDMM ODF bere data HARDI jako ODF v každém voxelu a řeší variační problém LDDMM v prostoru ODF. V oblasti informační geometrie tvoří prostor ODF riemannianskou řadu s metrikou Fisher-Rao. Pro účely mapování LDDMM ODF je zvolena reprezentace druhé odmocniny, protože je to jedna z nejúčinnějších reprezentací, které byly dosud nalezeny, protože různé riemannianské operace, jako jsou geodetika, exponenciální mapy a logaritmické mapy, jsou k dispozici v uzavřené formě. V následujícím textu označte odmocninu ODF ( ) jako , kde není záporná, aby byla zajištěna jedinečnost a . Variační problém pro párování předpokládá, že dva objemy ODF lze generovat z jednoho do druhého pomocí toků diffeomorphismů , což jsou řešení běžných diferenciálních rovnic vycházejících z mapy identity . Označme působení difeomorfismus na šablonu , , jsou příslušné souřadnice jednotkové sféře, a doména obraz, s cílem indexovaného podobně , , . ${\ displaystyle {\ sqrt {\ text {ODF}}}}$${\ displaystyle \ psi ({\ bf {s}})}$${\ displaystyle \ psi ({\ bf {s}})}$${\ Displaystyle \ int _ {{\ bf {s}} \ in {\ mathbb {S}} ^{2}} \ psi ^{2} ({\ bf {s}}) d {\ bf {s} } = 1}$${\ displaystyle \ phi _ {t}}$${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} (\ phi _ {t}), t \ in [0,1],}$${\ displaystyle \ phi _ {0} = {id}}$${\ Displaystyle \ phi _ {1} \ cdot \ psi _ {\ mathrm {temp}} ({\ bf {s}}, x)}$${\ displaystyle {\ bf {s}} \ v {{\ mathbb {S}}^{2}}}$${\ displaystyle x \ v X}$${\ displaystyle {{\ mathbb {S}}^{2}}}$${\ Displaystyle \ psi _ {\ mathrm {targ}} ({\ bf {s}}, x)}$${\ displaystyle {\ bf {s}} \ v {{\ mathbb {S}}^{2}}}$${\ displaystyle x \ v X}$

Skupinové působení diffeomorfismu na šablonu je dáno podle

${\ Displaystyle \ phi _ {1} \ cdot \ psi (x) \ doteq (D \ phi _ {1}) \ psi \ circ \ phi _ {1}^{-1} (x), x \ v X }$,

kde je jakobijan afinního transformovaného ODF a je definován jako ${\ displaystyle (D \ phi _ {1})}$${\ Displaystyle {\ begin {aligned} (D \ phi _ {1}) \ psi \ circle \ phi _ {1}^{-1} (x) = {\ sqrt {\ frac {\ det {{\ bigl (} D _ {\ phi _ {1}^{-1}} \ phi _ {1} {\ bigr)}^{-1}}} {\ left \ | {{\ bigl (} D _ {\ phi _ {1}^{-1}} \ phi _ {1} {\ bigr)}^{-1}} {\ bf {s}} \ right \ |^{3}}}} \ quad \ psi \ left ({\ frac {(D _ {\ phi _ {1}^{-1}} \ phi _ {1} {\ bigr)}^{-1} {\ bf {s}}} {\ | (D_ { \ phi _ {1}^{-1}} \ phi _ {1} {\ bigr)}^{-1} {\ bf {s}} \ |}}, \ phi _ {1}^{-1 } (x) \ vpravo). \ end {aligned}}}$

Toto skupinové působení diffeomorphismů na ODF přeorientuje ODF a odráží změny jak ve velikosti, tak ve směrech vzorkování v důsledku afinní transformace. Zaručuje, že objemový podíl vláken orientovaných na malou náplast musí po transformaci náplasti zůstat stejný. ${\ Displaystyle \ psi}$${\ displaystyle {\ bf {s}}}$

Variační problém LDDMM je definován jako

${\ displaystyle {\ begin {aligned} C (v) = \ inf _ {v: {\ dot {\ phi}} _ {t} = v_ {t} \ circle \ phi _ {t}, \ phi _ { 0} = {id}} \ int _ {0}^{1} \ int _ {X} Av_ {t} \ cdot v_ {t} dx \ dt+\ lambda \ int _ {x \ in \ Omega} \ | \ log _ {(D \ phi _ {1}) \ psi _ {\ mathrm {temp}} \ circ \ phi _ {1}^{-1} (x)} (\ psi _ {\ mathrm {targ} } (x)) \ | _ {(D \ phi _ {1}) \ psi _ {\ mathrm {temp}} \ circ \ phi _ {1}^{-1} (x)}^{2} dx \ end {aligned}}}$.

kde logaritmus je definován jako ${\ Displaystyle \ psi _ {1}, \ psi _ {2} \ in \ Psi}$

${\ Displaystyle {\ begin {aligned} \ | \ log _ {\ psi _ {1}} (\ psi _ {2}) \ | _ {\ psi _ {1}} = \ cos ^{-1} \ langle \ psi _ {1}, \ psi _ {2} \ rangle = \ cos ^{-1} \ left (\ int _ {{\ bf {s}} \ in {\ mathbb {S}} ^{2 }} \ psi _ {1} ({\ bf {s}}) \ psi _ {2} ({\ bf {s}}) d {\ bf {s}} \ vpravo), \ end {zarovnáno}} }$

kde je normální bodový součin mezi body v kouli pod metrikou. ${\ Displaystyle \ langle \ cdot, \ cdot \ rangle}$${\ displaystyle \ mathrm {L} ^{2}}$

Tento algoritmus mapování LDDMM-ODF byl široce používán ke studiu degenerace mozkové bílé hmoty při stárnutí, Alzheimerově chorobě a vaskulární demenci. Atlas bílé hmoty mozku generovaný na základě ODF je konstruován pomocí Bayesovského odhadu. Regresní analýza na ODF je vyvinuta v prostoru ODF potrubí v.

Metamorfóza

Principem variace, kterou model oběžné dráhy představuje, je změna souřadnic. Pro nastavení, ve kterém páry obrazů nesouvisejí s diffeomorphismy, ale mají fotometrické variace nebo variace obrazu, které nejsou představovány šablonou, bylo zavedeno aktivní modelování vzhledu , původně od Edwards-Cootes-Taylor a v 3D lékařském zobrazování v. výpočetní anatomie, ve které byla studována metrika na anatomické oběžné dráze, byla do obrazových modelů s magnetickou rezonancí zavedena metamorfóza pro modelování struktur, jako jsou nádory a fotometrické změny, které nejsou v šabloně, s mnoha následnými vývojy rozšiřujícími rámec metamorfózy.

Pro přizpůsobení obrazu rámec metamorfózy obrazu zvětšuje akci tak, že s akcí . V tomto nastavení metamorfóza kombinuje jak transformaci výpočetní anatomie na diffeomorfní souřadnicový systém, tak technologie raného morfování, které pouze vybledly nebo upravily samotnou fotometrickou nebo obrazovou intenzitu. ${\ displaystyle t \ mapsto (\ phi _ {t}, I_ {t})}$${\ Displaystyle \ phi _ {t} \ cdot I_ {t} \ doteq I_ {t} \ circ \ phi _ {t}^{-1}}$

Pak má problém shody formu s hraničními podmínkami rovnosti:

${\ Displaystyle \ min _ {(v, I)} {\ frac {1} {2}} \ int _ {0}^{1} \ left (\ int _ {X} Av_ {t} \ cdot v_ { t} dx+\ | {\ tečka {I}} _ {t} \ circ \ phi _ {t}^{-1} \ |^{2}/\ sigma^{2} \ vpravo) \, dt {\ text {podléhá}} \ \ phi _ {0} = id, I_ {0} = {\ text {fixed}}, I_ {1} = {\ text {fixed}}}$

Odpovídající orientační body, křivky, povrchy

Transformace souřadnicových systémů na základě bodů orientačního bodu nebo referenčních značek pochází z Booksteinovy ​​rané práce na metodách malých deformačních spline pro interpolaci korespondencí definovaných referenčními body do dvojrozměrného nebo trojrozměrného prostoru pozadí, ve kterém jsou definovány referenční body. Metody velkých deformačních mezníků se objevily koncem devadesátých let. Výše uvedený obrázek zobrazuje řadu orientačních bodů spojených se třemi strukturami mozku, amygdala, entorhinální kůra a hippocampus.

Porovnávání geometrických objektů, jako jsou neoznačené bodové distribuce, křivky nebo povrchy, je dalším běžným problémem ve výpočetní anatomii. I v diskrétním prostředí, kde jsou tyto obvykle uvedeny jako vrcholy se sítěmi, neexistují žádné předem určené shody mezi body na rozdíl od situace orientačních bodů popsaných výše. Z teoretického hlediska, zatímco jakýkoliv submanifold v , může být nastaven v místních grafech , všechny reparametrizations těchto grafů dát geometricky stejnou potrubí. Proto na počátku výpočetní anatomie vyšetřovatelé identifikovali nutnost invariantních reprezentací parametrizace. Jedním nepostradatelným požadavkem je, aby termín shody koncového bodu mezi dvěma dílčími rozdělovači byl nezávislý na jejich parametrizaci. Toho lze dosáhnout pomocí konceptů a metod převzatých z teorie geometrických měření , zejména proudů a varifoldů, které byly široce používány pro přizpůsobení křivek a povrchů. ${\ displaystyle X}$${\ displaystyle {\ mathbb {R}}^{3}}$${\ Displaystyle d = 1,2,3}$${\ Displaystyle m: u \ in U \ subset {\ mathbb {R}}^{0,1,2,3} \ rightarrow {\ mathbb {R}}^{3}}$

Shodování orientačních bodů nebo bodů s korespondencí

Variabilním problémem, označeným jako orientační tvar koncovým bodem , se stává ${\ Displaystyle X \ doteq \ {x_ {1}, \ tečky, x_ {n} \} \ podmnožina {\ mathbb {R}}^{3}}$${\ Displaystyle E (\ phi _ {1}) \ doteq \ textstyle \ sum _ {i} \ displaystyle \ | \ phi _ {1} (x_ {i})-x_ {i}^{\ prime} \ | ^{2}}$

.${\ Displaystyle {\ begin {matrix} & \ \ \ \ min _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^{-1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int (Av_ {t} | v_ {t}) dt+{\ frac {1} {2}} \ sum _ {i} \ | \ phi _ {1} (x_ {i} ) -x_ {i}^{\ prime} \ |^{2} \ end {matrix}}}$

( Shoda s orientačními body )

Geodetická eulerovská hybnost je zobecněná funkce , podporovaná na orientační sadě ve variačním problému. Podmínka koncového bodu při zachování implikuje počáteční hybnost identity skupiny: ${\ Displaystyle \ displaystyle Av_ {t} \ in V^{*} \ textstyle, t \ in [0,1]}$

${\ Displaystyle {\ begin {cases} & {\ text {Endpoint Condition:}} \ \ \ \ Av_ {1} = \ sum _ {i = 1}^{n} p_ {1} (i) \ delta _ {\ phi _ {1} (x_ {i})}, p_ {1} (i) = (x_ {i}^{\ prime}-\ phi _ {1} (x_ {i})) \, \\ & {\ text {Conservation:}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Av_ {t} = \ sum _ {i = 1}^{n} p_ {t} (i) \ delta _ {\ phi _ {t} (x_ {i})}, \ p_ {t} (i) = (D \ phi _ {t1}) _ {| \ phi _ {t} (x_ {i}) }^{T} p_ {1} (i) \, \ \ phi _ {t1} \ doteq \ phi _ {1} \ circ \ phi _ {t}^{-1} \, \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Av_ {0} = \ součet _ {i} \ delta _ {x_ {i}} (\ cdot) p_ {0} (i) \ {\ text {with}} \ \ p_ {0} (i) = (D \ phi _ {1}) _ {| x_ {i}}^{T} (x_ {i}^{\ prime}-\ phi _ {1} (x_ {i})) \ end {případy}}}$

Je uveden iterační algoritmus pro velké deformační diffeomorfní metrické mapování orientačních bodů .

Měření shody: neregistrované orientační body

Glaunes a spolupracovníci poprvé zavedli diffeomorfní párování množin bodů v obecném nastavení odpovídajících distribucí. Na rozdíl od orientačních bodů to zahrnuje zejména situaci vážených mračen bodů bez předdefinovaných shod a případně různých kardinalit. Šablony a cílové diskrétní bodové mraky jsou reprezentovány jako dva vážené součty Diracs a žijí v prostoru podepsaných opatření pro . Prostor je vybaven Hilbert metrikou získanou z reálného kladného jádra na , v němž jsou uvedeny následující normy: ${\ Displaystyle \ mu _ {m} = \ sum _ {i = 1}^{n} \ rho _ {i} \ delta _ {x_ {i}}}$${\ Displaystyle \ mu _ {m^{\ prime}} = \ sum _ {i = 1}^{n^{\ prime}} \ rho _ {i}^{\ prime} \ delta _ {x_ {i }^{\ prime}}}$${\ displaystyle \ mathbb {R} ^{3}}$${\ Displaystyle k (x, y)}$${\ displaystyle \ mathbb {R} ^{3}}$

${\ Displaystyle \ | \ mu _ {m} \ | _ {\ mathrm {mea}}^{2} = \ sum _ {i, j = 1}^{n} \ rho _ {i} \ rho _ { j} k (x_ {i}, x_ {j})}$

Problém shody mezi šablonami a mračnem cílových bodů lze poté formulovat pomocí této metriky jádra pro termín shody koncového bodu:

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circle \ phi ^{-1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int ( Av_ {t} \ mid v_ {t}) \, dt+{\ frac {1} {2}} \ | \ mu _ {\ phi _ {1} \ cdot m}-\ mu _ {m^{\ prime }} \ | _ {\ mathrm {mea}}^{2}}$

kde je distribuce transportována deformací. ${\ Displaystyle \ mu _ {\ phi _ {1} \ cdot m} = \ sum _ {i = 1}^{n} \ rho _ {i} \ delta _ {\ phi _ {1} (x_ {i })}}$

Shoda křivek

V jednorozměrném případě může být křivka ve 3D reprezentována vložením a skupinová akce Diff se stane . Korespondence mezi křivkami a vloženími není jedna k jedné, protože jakákoli reparametrizace pro diffeomorfismus intervalu [0,1] představuje geometricky stejnou křivku. Aby byla zachována tato invariance v termínu shody koncových bodů, lze zvážit několik rozšíření předchozího přístupu shody 0-dimenzionální míry. ${\ Displaystyle m: u \ in [0,1] \ rightarrow {\ mathbb {R}}^{3}}$${\ Displaystyle \ phi \ cdot m = \ phi \ circ m}$${\ Displaystyle m \ circ \ gamma}$${\ displaystyle \ gamma}$

• Křivka s proudy

V situaci orientovaných křivek poskytují proudy efektivní nastavení pro konstrukci invariantních odpovídajících výrazů. V takové reprezentaci jsou křivky interpretovány jako prvky funkčního prostoru duální k prostorovým vektorovým polím a porovnávány prostřednictvím norem jádra v těchto prostorech. Shoda dvou křivek a zápisů nakonec jako variační problém ${\ displaystyle m}$${\ displaystyle m^{\ prime}}$

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circle \ phi ^{-1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int ( Av_ {t} \ mid v_ {t}) \, dt+{\ frac {1} {2}} \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m}-{\ mathcal { C}} _ ​​{m^{\ prime}} \ | _ {\ mathrm {cur}}^{2}}$

s termínem koncového bodu je získán z normy ${\ Displaystyle E (\ phi _ {1}) = \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m}-{\ mathcal {C}} _ ​​{m^{\ prime} } \ | _ {\ mathrm {cur}}^{2}/2}$

${\ Displaystyle \ | {\ mathcal {C}} _ ​​{m} \ | _ {\ mathrm {cur}}^{2} = \ int _ {0}^{1} \ int _ {0}^{1 } K_ {C} (m (u), m (v)) \ částečný m (u) \ cdot \ částečný m (v) \, du \, dv}$

derivát je tečný vektor křivky a dané maticové jádro . Takové výrazy jsou invariantní vůči jakýmkoli pozitivním reparametrizacím a , a proto stále závisí na orientaci těchto dvou křivek. ${\ Displaystyle \ partial m (u)}$${\ displaystyle K _ {\ mathcal {C}}}$${\ displaystyle {\ mathbb {R}}^{3}}$${\ displaystyle m}$${\ displaystyle m '}$

• Křivka s varifoldem

Varifold je alternativou proudů, když se orientace stává problémem, například v situacích zahrnujících více svazků křivek, pro které nelze definovat „konzistentní“ orientaci. Varifolds přímo prodlužují 0-rozměrné míry přidáním extra tangentního směru prostoru k poloze bodů, což vede k reprezentaci křivek jako míry na součinu a Grassmannian všech přímek v . Problém shody mezi dvěma křivkami pak spočívá v nahrazení výrazu pro shodu koncového bodu normami různých tvarů: ${\ displaystyle {\ mathbb {R}}^{3}}$${\ displaystyle {\ mathbb {R}}^{3}}$${\ Displaystyle E (\ phi _ {1}) = \ | {\ mathcal {V}} _ {\ phi _ {1} \ cdot m}-{\ mathcal {V}} _ {m^{\ prime} } \ | _ {cur}^{2}/2}$

${\ Displaystyle \ | {\ mathcal {V}} _ {m} \ | _ {var}^{2} = \ int _ {0}^{1} \ int _ {0}^{1} k _ {\ mathbb {R} ^{3}} (m (u), m (v)) k _ {\ mathbf {Gr}} \ left ([\ částečné m (u)], [\ částečné m (v)] \ vpravo ) {|} \ částečné m (u) {|} {|} \ částečné m (v) {|} \, du \, dv}$

kde je neorientovaná přímka směrovaná tečným vektorem a dvěma skalárními jádry na Grassmannian. Vzhledem k inherentní neorientované povaze Grassmannovy reprezentace jsou tyto výrazy invariantní vůči pozitivním a negativním reparametrizacím. ${\ Displaystyle [\ partial m (u)]}$${\ Displaystyle \ partial m (u)}$${\ Displaystyle k _ {\ mathbb {R} ^{3}}, k _ {\ mathbf {Gr}}}$${\ displaystyle \ mathbb {R} ^{3}}$

Přizpůsobení povrchu

Shoda povrchů má mnoho podobností s křivkami. Povrchy v jsou v místních grafech parametrizovány vložením , přičemž všechny reparametrizace s odlišným tvarem U jsou geometricky ekvivalentní. Proudy a varifold lze také použít k formalizaci přizpůsobení povrchu. ${\ displaystyle {\ mathbb {R}}^{3}}$${\ Displaystyle m: u \ v U \ podmnožina {\ mathbb {R}}^{2} \ rightarrow {\ mathbb {R}}^{3}}$${\ Displaystyle m \ circ \ gamma}$${\ displaystyle \ gamma}$

• Přizpůsobení povrchu proudům

Orientované povrchy mohou být reprezentovány jako 2-proudy, které jsou duální až diferenciální 2-formy. V jednom lze dále identifikovat 2-formy s vektorovými poli prostřednictvím standardního klínového součinu 3D vektorů. V tomto nastavení shoda povrchu opět zapíše: ${\ displaystyle {\ mathbb {R}}^{3}}$

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circle \ phi ^{-1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int ( Av_ {t} \ mid v_ {t}) \, dt+{\ frac {1} {2}} \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m}-{\ mathcal { C}} _ ​​{m^{\ prime}} \ | _ {\ mathrm {cur}}^{2}}$

s termínem koncového bodu daným normou ${\ Displaystyle E (\ phi _ {1}) = \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m}-{\ mathcal {C}} _ ​​{m^{\ prime} } \ | _ {\ mathrm {cur}}^{2}/2}$

${\ Displaystyle \ | {\ mathcal {C}} _ ​​{m} \ | _ {\ mathrm {cur}}^{2} = \ iint _ {U \ times U} K_ {C} (m (u), m (v)) {\ vec {n}} (u) \ cdot {\ vec {n}} (v) \, du \, dv}$

s normálním vektorem na povrch parametrizovaným . ${\ Displaystyle {\ vec {n}} = \ částečné _ {u_ {1}} m \ klín \ částečné _ {u_ {2}} m}$${\ displaystyle m}$

Tento algoritmus mapování povrchu byl validován pro mozkové kortikální povrchy proti CARET a FreeSurfer. Mapování LDDMM pro víceúrovňové povrchy je popsáno v.

• Sladění povrchu pomocí varifoldů

U neorientovatelných nebo neorientovaných povrchů je často vhodnější rámová konstrukce. Identifikace parametrické plochy varifoldem v prostoru měr na součinu a Grassmannian, jeden jednoduše nahradí předchozí aktuální metriku : ${\ displaystyle m}$${\ displaystyle {\ mathcal {V}} _ {m}}$${\ displaystyle {\ mathbb {R}}^{3}}$${\ displaystyle \ | {\ mathcal {C}} _ ​​{m} \ | _ {\ mathrm {cur}}^{2}}$

${\ Displaystyle \ | {\ mathcal {V}} _ {m} \ | _ {\ mathrm {var}} ^{2} = \ iint _ {U \ times U} k _ {\ mathbb {R} ^{3 }} (m (u), m (v)) k _ {\ mathbf {Gr}} \ left ([{\ vec {n}} (u)], [{\ vec {n}} (v)] \ vpravo) {|} {\ vec {n}} (u) {|} {|} {\ vec {n}} (v) {|} \, du \, dv}$

kde je (neorientovaná) přímka směrovaná normálním vektorem na povrch. ${\ displaystyle [{\ vec {n}} (u)]}$

Růst a atrofie z podélných časových řad

Existuje mnoho nastavení, ve kterých existuje řada měření, časová řada, ke které budou přiřazeny a přeneseny základní souřadnicové systémy. K tomu dochází například v modelech dynamického růstu a atrofie a sledování pohybu, které byly prozkoumány v části Pozorovaná časová sekvence je dána a cílem je odvodit časový tok geometrické změny souřadnic přenášejících exempláře nebo templáře přes období pozorování .

Obecný problém shody časových řad považuje sérii časů za . Tok optimalizuje v řadě nákladů, což dává problémy s optimalizací formuláře ${\ Displaystyle 0 <t_ {1} <\ dots t_ {K} = 1}$${\ Displaystyle E (t_ {k}), k = 1, \ tečky, K}$

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^{-1}, \ phi _ {0} = id} C (\ phi) \ doteq {\ frac { 1} {2}} \ int _ {0}^{1} (Av_ {t} \ mid v_ {t}) \, dt+\ sum _ {k = 1}^{K} E (\ phi _ {t_ {k}})}$.

Dosud byla nabídnuta nejméně tři řešení, kusová geodetická, hlavní geodetická a splajny.

Náhodný orbitální model výpočetní anatomie

Excentrické modelu výpočetní anatomie poprvé objevil v modelování změnu souřadnic spojených s náhodnosti skupiny působící na šablonách, které indukuje náhodnosti na zdroji obrazu v anatomické oběžné dráze tvarů a forem a následné pozorování přes lékařské zobrazovací zařízení. Takový model náhodné oběžné dráhy, ve kterém náhodnost na skupině vyvolává náhodnost na obrázcích, byl zkoumán pro speciální euklidovskou skupinu pro rozpoznávání objektů v.

Na obrázku je znázorněno zobrazení náhodných oběžných drah kolem každého příkladu, generované randomizací toku generováním počátečního pole tečného prostorového vektoru na identitě a generováním náhodného objektu . ${\ displaystyle m_ {0} \ v {\ mathcal {M}}}$${\ displaystyle v_ {0} \ v V}$${\ Displaystyle n \ doteq Exp_ {id} (v_ {0}) \ cdot m_ {0} \ in {\ mathcal {M}}}$

Model s náhodnou oběžnou dráhou indukuje předchozí tvary a obrázky podmíněné konkrétním atlasem . K tomu generativní model generuje průměrné pole jako náhodnou změnu souřadnic šablony podle , kde se diffeomorfní změna souřadnic generuje náhodně prostřednictvím geodetických toků. V dosavadním stavu na náhodných transformací na se indukuje proud , s zkonstruován jako Gaussova náhodné pole před . Hustota náhodných pozorovatelných na výstupu senzoru je dána vztahem ${\ displaystyle I \ v {\ mathcal {I}}}$${\ displaystyle I_ {a} \ v {\ mathcal {I}}}$${\ displaystyle I}$${\ Displaystyle I \ doteq \ phi \ cdot I_ {a}}$${\ displaystyle \ pi _ {Diff} (d \ phi)}$${\ displaystyle Diff_ {V}}$${\ displaystyle Exp_ {id} (v)}$${\ displaystyle v \ v V}$${\ displaystyle \ pi _ {V} (dv)}$${\ Displaystyle I^{D} \ v {\ mathcal {I}}^{D}}$

${\ Displaystyle p (I^{D} | I_ {a}) = \ int _ {V} p (I^{D} | Exp_ {id} (v) \ cdot I_ {a}) \ pi _ {V } (dv) \.}$

Na obrázku vpravo na kreslené oběžné dráze jsou náhodné spreje subkortikálních variet generovaných randomizací vektorových polí podporovaných přes submanifolds. ${\ displaystyle v_ {0}}$

Bayesovský model výpočetní anatomie

Centrálním statistickým modelem výpočetní anatomie v kontextu lékařského zobrazování byl model zdrojového kanálu Shannonovy teorie ; zdrojem je deformovatelná šablona obrazů , kanálové výstupy jsou zobrazovací senzory s pozorovatelnými (viz obrázek). ${\ displaystyle I \ v {\ mathcal {I}}}$${\ Displaystyle I^{D} \ v {\ mathcal {I}}^{\ mathcal {D}}}$

Diskuse viz Bayesovský model výpočetní anatomie (i) Odhad MAP s více atlasy, (ii) MAP segmentace s více atlasy, MAP odhad šablon z populací.

Teorie statistických tvarů ve výpočetní anatomii

Tvar ve výpočetní anatomii je lokální teorie, která indexuje tvary a struktury do šablon, na které jsou bijektivně mapovány. Statistický tvar ve výpočetní anatomii je empirická studie diffeomorfních korespondencí mezi populacemi a běžnými souřadnicovými systémy šablon. Jedná se o výrazný odklon od Procrustesových analýz a teorií tvarů, které propagoval David G. Kendall v tom, že ústřední skupinou Kendallových teorií jsou skupiny Lieových konečných dimenzí, zatímco teorie tvaru ve výpočetní anatomii se zaměřily na skupinu diffeomorfismu, která první řád přes jakobiány lze považovat za pole-tedy nekonečné dimenze-nízko dimenzionálních Lieových skupin měřítka a rotací.

Model náhodných orbit poskytuje přirozené prostředí pro pochopení empirických tvarů a statistik tvarů v rámci výpočetní anatomie, protože nelinearita indukovaného zákona pravděpodobnosti anatomických tvarů a forem je indukována redukcí na vektorová pole v tangentovém prostoru při identitě skupina diffeomorfismu. Postupný tok Eulerovy rovnice indukuje náhodný prostor tvarů a forem . ${\ displaystyle m \ v {\ mathcal {M}}}$${\ displaystyle v_ {0} \ v V}$${\ displaystyle Exp_ {id} (v_ {0}) \ cdot m \ v {\ mathcal {M}}}$

Provádění empirických statistik v tomto tangentovém prostoru na identitě je přirozeným způsobem vyvolání zákonů pravděpodobnosti ve statistikách tvaru. Vzhledem k tomu, že vektorová pole i eulerovská hybnost jsou v Hilbertově prostoru, přirozený model je jedním z gaussovských náhodných polí, takže vzhledem k dané testovací funkci jsou pak vnitřní produkty s testovacími funkcemi gaussovsky distribuovány s průměrem a kovariancí. ${\ displaystyle Av_ {0}}$${\ Displaystyle w \ v V}$

To je znázorněno na přiloženém obrázku, kde jsou subkortikální mozkové struktury znázorněny v dvourozměrném souřadnicovém systému založeném na vnitřních produktech jejich počátečních vektorových polí, která je generují z šablony, je zobrazeno v 2-dimenzionálním rozpětí Hilbertova prostoru.

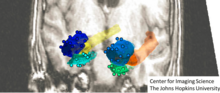
Odhad šablony z populací

Studium tvaru a statistiky v populacích jsou lokální teorie, indexování tvarů a struktur do šablon, na které jsou bijektivně mapovány. Statistickým tvarem je pak studium diffeomorfních korespondencí vzhledem k šabloně. Základní operací je generování šablon z populací, které odhadují tvar, který odpovídá populaci. Existuje několik důležitých metod pro generování šablon, včetně metod založených na Frechetově průměrování a statistických přístupů založených na algoritmu maximalizace očekávání a Bayesových náhodných orbitálních modelech výpočetní anatomie. Na doprovodném obrázku je znázorněna subkortikální rekonstrukce šablony z populace subjektů MRI.

Software pro diffeomorfní mapování

Softwarové sady obsahující různé algoritmy dvojfázového mapování zahrnují následující:

• Mravenci
• DARTEL Morfometrie na bázi Voxelu
• DEFORMETRICA
• Démoni
• LDDMM Velké deformační diffeomorfní metrické mapování
• LDDMM na základě rámcového jádra
• Stacionární LDDMM

Cloudový software

• MRICloud

Viz také

• Bayesovský odhad šablon ve výpočetní anatomii
• Výpočetní neuroanatomie
• Analýza geometrických dat
• Velké deformační diffeomorfní metrické mapování
• Procrustes analýza
• Riemannova metrika a Lieova závorka ve výpočetní anatomii
• Analýza tvaru (disambiguation)
• Statistická analýza tvaru

Reference