Automorfismus - Automorphism

Automorphism z Klein čtyři skupiny zobrazena jako mapování mezi dvěma grafy Cayley , permutací v notaci cyklu , a mapování mezi dvěma tabulkami Cayley .

V matematice , An automorphism je izomorfismus od matematický objekt sám na sebe. Je to v jistém smyslu symetrie objektu a způsob mapování objektu k sobě samému při zachování celé jeho struktury. Množina všech automorphisms objektu tvoří skupinu , která se nazývá automorphism skupina . Je to, volně řečeno, symetrická skupina objektu.

Definice

V kontextu abstraktní algebry je matematickým objektem algebraická struktura , jako je skupina , kruh nebo vektorový prostor . Automorphism je prostě bijective homomorphism objektu se sebou samým. (Definice homomorfismu závisí na typu algebraické struktury; viz například skupinový homomorfismus , kruhový homomorfismus a lineární operátor ).

Morphism identity ( mapping identita ) se nazývá triviální automorphism v některých kontextech. Respektive jiné (neidentifikační) automorfismy se nazývají netriviální automorfismy .

Přesná definice automorfismu závisí na typu dotyčného „matematického objektu“ a na tom, co přesně představuje „izomorfismus“ tohoto objektu. Nejobecnějším prostředím, ve kterém mají tato slova význam, je abstraktní obor matematiky nazývaný teorie kategorií . Teorie kategorií se zabývá abstraktními objekty a morfismem mezi těmito objekty.

V teorii kategorie, An automorphism je endomorphism (tj morfismus od objektu k sobě), která je také izomorfismus (ve kategorické slova smyslu, což znamená, že existuje pravý a levý inverzní endomorfismů).

Toto je velmi abstraktní definice, protože v teorii kategorií nejsou morfismy nutně funkcemi a objekty nemusí být nutně množinami. Ve většině konkrétních nastavení však budou objekty sady s nějakou další strukturou a morfismy budou funkce zachovávající tuto strukturu.

Automorfická skupina

V případě, že automorfismy objektu X tvoří jeden celek (namísto správné třídy ), pak tvoří skupinu pod složením z morphisms . Tato skupina se nazývá automorphism skupina z X .

Uzavření: Složení dvou automorfismů je dalším automorfismem.
Asociativita: Součástí definice kategorie je asociativní složení morfismů.
Identita: Identita je morfismus identity od objektu k sobě samému, což je automorfismus.
Inverses: Podle definice má každý izomorfismus inverzi, která je také izomorfismem, a protože inverze je také endomorfismem stejného objektu, jedná se o automorfismus.

Skupina automorfismu objektu X v kategorii C se označuje Aut _C ( X ), nebo jednoduše Aut ( X ), pokud je kategorie jasná z kontextu.

Příklady

V teorii množin je libovolná permutace prvků množiny X automorfismem. Automorphism skupina X se také nazývá symetrický skupinu na X .
V elementární aritmetice má množina celých čísel , Z , považovaná za přidanou skupinu, jedinečný netriviální automorfismus: negace. Považuje se za prsten, ale má pouze banální automorfismus. Obecně řečeno, negace je automorfismus jakékoli abelianské skupiny , ale nikoli prstence nebo pole.
Skupinový automorfismus je skupinový izomorfismus ze skupiny k sobě samému. Neformálně jde o permutaci prvků skupiny, takže struktura zůstane nezměněna. Pro každou skupinu G existuje přirozená skupina homomorphism G → Aut ( G ), jehož obraz je skupina Inn ( G ) z vnitřních automorphisms a jehož jádro je centrem z G . Pokud má tedy G triviální centrum, může být vloženo do vlastní skupiny automorfismu.
V lineární algebře , endomorphism z vektorového prostoru V, je lineární operátor V → V . Automorphism je regulární lineární operátor na V . Když je vektorový prostor konečně-dimenzionální, skupina automorfismu V je stejná jako obecná lineární skupina GL ( V ). (Algebraická struktura všech endomorfismů V je sama algebra na stejném základním poli jako V , jehož invertibilní prvky přesně sestávají z GL ( V ).)
Polní automatorfismus je bijektivní kruhový homomorfismus z pole k sobě samému. V případě racionálních čísel ( Q ) a reálných čísel ( R ) neexistují žádné netriviální polní automatorfismy. Některá podpole R mají netriviální polní automatorfismy, které se však nevztahují na všechna R (protože nemohou zachovat vlastnost čísla, které má v R druhou odmocninu ). V případě komplexních čísel , C , existuje jedinečný netriviální automorfismus, který posílá R do R : komplexní konjugace , ale existuje nekonečně ( nespočetně ) mnoho „divokých“ automorfismů (za předpokladu axiomu volby ). Polní automatorfismy jsou důležité pro teorii rozšíření pole , zejména rozšíření Galois . V případě rozšíření Galois L / K se podskupina všech automorfismů L fixujících K bodově nazývá Galoisova skupina rozšíření.
Automorphism skupina čtveřic ( H ) jako prsten jsou vnitřní automorphisms, podle věty Skolem-Noether : mapy formy a ↦ bab ⁻¹ . Tato skupina je izomorfní vůči SO (3) , skupině rotací v trojrozměrném prostoru.
Automorfická skupina oktonionů ( O ) je výjimečná Lieova skupina G ₂ .
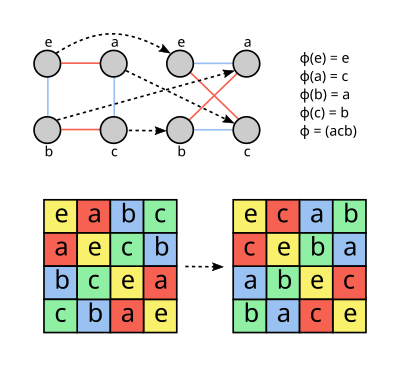
V teorii grafů je automorfismus grafu permutací uzlů, která zachovává hrany a ne-hrany. Zejména pokud jsou dva uzly spojeny hranou, jsou také jejich obrazy pod permutací.
V geometrii lze automorfismus nazvat pohybem prostoru. Používá se také odborná terminologie:
- V metrické geometrii je automorfismus samoizometrie . Skupině automorfismu se také říká skupina izometrie .
- V kategorii Riemannův povrchů je automorfismus biholomorfní mapa (nazývaná také konformní mapa ), od povrchu k sobě samému. Například automorfismy Riemannovy koule jsou Möbiovy transformace .
- Automorfismus diferencovatelného potrubí M je difeomorfismus od M k sobě samému. Skupina automorfismu je někdy označována jako Diff ( M ).
- V topologii se morfismy mezi topologickými prostory nazývají spojité mapy a automorfismus topologického prostoru je homeomorfismus prostoru pro sebe nebo self-homeomorfismus (viz skupina homeomorfismu ). V tomto příkladu nestačí, aby morfismus byl bijektivní, aby byl izomorfismem.

Dějiny

Jeden z prvních skupinových automorfismů (automorfismus skupiny, nikoli pouze skupina automatorfismů bodů) dal irský matematik William Rowan Hamilton v roce 1856 ve svém ikonickém kalkulu , kde objevil řád dva automorfismus, kde napsal:

to je tedy nový pátý kořen jednoty, spojený s bývalým pátým kořenem vztahy dokonalé vzájemnosti. ${\ displaystyle \ mu}$ ${\ displaystyle \ lambda}$

Vnitřní a vnější automorfismy

V některých kategoriích - zejména ve skupinách , kruzích a Lieových algebrách - je možné oddělit automorfismy do dvou typů, nazývaných „vnitřní“ a „vnější“ automorfismy.

V případě skupin jsou vnitřní automorfismy konjugace prvky samotné skupiny. Pro každý prvek A skupiny G , konjugace podle je operace φ _a : G → G dán φ ( g ) = aga ^-1 (nebo ^-1ga , použití se liší). Lze snadno ověřit, že konjugace pomocí a je skupinový automorfismus. Vnitřní automorfismy tvoří normální podskupinu Aut ( G ), označenou Inn ( G ); tomu se říká Goursatovo lemma .

Ostatní automorfismy se nazývají vnější automorfismy . Kvocient skupina Aut ( G ) / Inn ( G ) je obvykle označován Z ( G ); netriviálními prvky jsou kosety, které obsahují vnější automorfismy.

Stejná definice platí v jakémkoli unitálním kruhu nebo algebře, kde a je jakýkoli invertibilní prvek . U Lieových algeber se definice mírně liší.

Viz také

Reference

^ PJ Pahl, R Damrath (2001). „§7.5.5 Automorfismy“ . Matematické základy výpočetního inženýrství (překlad Felix Pahl ed.). Springer. p. 376. ISBN 3-540-67995-2.
^ Yale, Paul B. (květen 1966). „Automorfismy komplexních čísel“ (PDF) . Matematický časopis . 39 (3): 135–141. doi : 10,2307 / 2689301 . JSTOR 2689301 .
^ Lounesto, Pertti (2001), Clifford Algebras and Spinors (2. vyd.), Cambridge University Press, s. 22–23, ISBN 0-521-00551-5
^ Příručka algebry , 3 , Elsevier , 2003, s. 453
^ Sir William Rowan Hamilton (1856). „Memorandum o respektování nového systému kořenů jednoty“ (PDF) . Filozofický časopis . 12 : 446.

externí odkazy

[Pahl-1] PJ Pahl, R Damrath (2001). „§7.5.5 Automorfismy“ . Matematické základy výpočetního inženýrství (překlad Felix Pahl ed.). Springer. p. 376. ISBN 3-540-67995-2.

[2] Yale, Paul B. (květen 1966). „Automorfismy komplexních čísel“ (PDF) . Matematický časopis . 39 (3): 135–141. doi : 10,2307 / 2689301 . JSTOR 2689301 .

[3] Lounesto, Pertti (2001), Clifford Algebras and Spinors (2. vyd.), Cambridge University Press, s. 22–23, ISBN 0-521-00551-5

[4] Příručka algebry , 3 , Elsevier , 2003, s. 453

[5] Sir William Rowan Hamilton (1856). „Memorandum o respektování nového systému kořenů jednoty“ (PDF) . Filozofický časopis . 12 : 446.

Languages

In other projects